Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Méca : Ressort avec Frottement

Posté par
Tiboz 24-10-18 à 19:30

Bonjour !

Je suis en PCSI et pendant les vacances, ma prof de physique m'a donné un DM.
Il comporte 2 parties : la première est une partie sans les frottements et la seconde avec.

C'est sur cette seconde partie que je bloque...

Voici l'énoncé de la seconde partie :
Glissement avec frottement : Réaction du support = R = N (composante normale) + T (composante tangentielle).
Les frottements entre solides sont décrit par les lois suivantes :
- Le point M peut être maintenu en place par l'existence de la réaction tangentielle T, à condition que celle-ci reste limitée par l'inégalité : T <= fN
- Si cette condition n'est pas réalisable, alors le point M glisse et le frottement est régi par la loi de Coulomb : T est opposé au glissement et T=fN.

Les premières questions de cette partie sont faciles mais je bloque à celle-là :
- On suppose cette condition non réalisée, le point M se mettant à glisser dans le sens des x décroissants, trouver l'équation du mouvement du point M jusqu'à ce qu'il s'arrête pour la première fois.

C'est cette partie (en gras) qui me gêne...

Dans la question précédente, j'ai établi une condition permettant au point M, étant maintenu immobile, de rester immobile quand on le lâche.
Cependant, je ne vois pas du tout comment l'utiliser dans cette question vu qu'il s'agit d'une inégalité (si la position x est comprise entre deux valeur, alors le point M est en équilibre)

J'aurai bien aimé vous joindre l'image de mon brouillon (qui est assez propre) mais apparemment, on n'a pas le droit (je suis nouveau ici).

Merci d'avance !

Posté par
vanoisere : Méca : Ressort avec Frottement 24-10-18 à 19:44

Bonsoir
Pas facile de t'aider sans un énoncé complet...
Quelques idées générales cependant :
heureusement, ton énoncé simplifie un peu la réalité en considérant que le coefficient de frottement statique est égal au coefficient de frottement dynamique. Cela simplifie beaucoup les calculs.
Tu peux écrire l'équation différentielle résultant de l'application de la RFD en supposant que la vitesse ne change pas de sens (équation valide pendant une demie pseudo période). Tu en déduit x(t) et v(t) valide pendant une première demie pseudo période. Pour la pseudo période suivante, la force de frottement change de sens, les équations sont différentes.
Si je comprends bien, il s'agit d'étudier l'oscillateur avec frottement solide. Tu devrais arriver à démontrer trois différences importantes par rapport au mouvement de l'oscillateur avec frottement visqueux :
La pseudo période est égale à la période propre
La diminution d'amplitude en une pseudo période reste fixe
L'arrêt définitif ne se fait pas nécessairement lorsque le ressort a sa longueur à vide (en supposant l'oscillateur horizontal).
Sous toute réserve...

Posté par
Tibozre : Méca : Ressort avec Frottement 24-10-18 à 19:52

Salut vanoise !

Il s'agit bien d'un oscillateur horizontal !
Je comprends la question dans ce sens:
- Il faut déterminer l'équation de mouvement du point M jusqu'à ce qu'il s'arrête mais sans osciller (on tend le ressort avec la masse et on le lâche ensuite) : cad que la Tension du ressort ( -k(l-lo) ) est inférieure à la force de frottement Tangentielle T

Mais je ne sais pas si c'est dans ce sens qu'il faut comprendre la question...

Posté par
vanoisere : Méca : Ressort avec Frottement 24-10-18 à 20:18

La question est-elle précédée de renseignements sur les conditions initiales ?

Posté par
Tibozre : Méca : Ressort avec Frottement 24-10-18 à 20:43

Non, aucune...

Si le point M s'arrête, sa vitesse est donc nulle, cad x' = 0 mais la vitesse n'intervient pas dans l'équa diff il me semble...

Posté par
vanoisere : Méca : Ressort avec Frottement 24-10-18 à 21:12

Pendant une demie pseudo période où la vitesse est positive, l'équation différentielle vérifiée par x=(l-lo) est :

\ddot{x}+\omega_{0}^{2}\cdot x=-f.g\quad avec\quad\omega_{0}=\sqrt{\frac{k}{m}}
Tu peux résoudre cette équation obtenant ainsi x=f(t) en choisissant par exemple comme conditions initiales :
xo=-A et vo = 0 avec A>0.
Ayant x= f(t) , il est facile d'obtenir v=g(t) et d'en déduire la date et la position telle que la vitesse s'annule pour la première fois. Pour la demie pseudo période suivante, il faut remplacer f par (-f) dans l'équation différentielle précédente...

Posté par
Tibozre : Méca : Ressort avec Frottement 24-10-18 à 21:21

vanoise @ 24-10-2018 à 21:12

Pendant une demie pseudo période où la vitesse est positive, l'équation différentielle vérifiée par x=(l-lo) est :

\ddot{x}+\omega_{0}^{2}\cdot x=-f.g\quad avec\quad\omega_{0}=\sqrt{\frac{k}{m}}
Tu peux résoudre cette équation obtenant ainsi x=f(t) en choisissant par exemple comme conditions initiales :
xo=-A et vo = 0 avec A>0.
Ayant x= f(t) , il est facile d'obtenir v=g(t) et d'en déduire la date et la position telle que la vitesse s'annule pour la première fois. Pour la demie pseudo période suivante, il faut remplacer f par (-f) dans l'équation différentielle précédente...


J'ai du mal à voir comment il peut y avoir au moins une oscillation...

Posté par
vanoisere : Méca : Ressort avec Frottement 24-10-18 à 21:34

C'est bien là que ton énoncé, au moins tel que tu le présentes, n'est pas clair. Pour qu'il y ait au moins une oscillation, il faut écarter le solide de masse m de sa position x= 0  en comprimant ou en allongeant le ressort suffisamment pour que, en l'abandonnant sans vitesse initiale, il exerce une force plus intense que celle de frottement. D'où le choix des conditions initiales de mon message précédent.
J'ai oublié de préciser dans mon message précédent :
k.A > f.m.g
D'autres choix de conditions initiales sont possibles bien sûr !

Posté par
Tibozre : Méca : Ressort avec Frottement 25-10-18 à 15:59

Je ne m'en sors pas, même si je pars du principe que le point M oscille avec des frottements, j'ai un problème sur mon équa diff...

Voici le schéma du système que j'ai établi (voir photo)

Méca : Ressort avec Frottement

Posté par
vanoisere : Méca : Ressort avec Frottement 25-10-18 à 18:15

L'équilibre est effectivement possible pour :

|x|<\frac{f.m.g}{k}
Ensuite, avec l'hypothèse des conditions initiales que j'ai faite, qu'est -ce qui te bloque pour t'empêcher d'obtenir l'équation différentielle de mon message du 24-10-18 à 21:12 complété par celui du  24-10-18 à 21:34 ?

Posté par
Tibozre : Méca : Ressort avec Frottement 25-10-18 à 22:14

Sur Ox j'ai :
m\ddot{x} + k(x_{0}-l_{0}) = \parallel \vec{T}\parallel = R_{x}

avec :
x = x_{0} - l_{0}

On retrouve bien :
\omega _{0} = \sqrt{\frac{k}{m}}

Mais je n'arrive pas à transformer le second membre...

Posté par
Tibozre : Méca : Ressort avec Frottement 25-10-18 à 22:17

Et je ne vois pas du tout le lien que je peux faire avec la question précédente pour savoir quand il s'arrête....

Il faudrait isoler x de mon équa diff et dire que : |x|<\frac{f.m.g}{k} ?

Mais dans ce cas, que deviendrai l'équation ?

Posté par
vanoisere : Méca : Ressort avec Frottement 25-10-18 à 23:20

Je pense que tu t'embrouilles avec l'expression de la tension du ressort. Si tu choisis l'origine des abscisses confondue avec la position du centre du solide de masse m dans le cas où l=lo (longueur à vide du ressort), il faut écrire que le ressort exerce à chaque une force de rappel qui tend à ramener le solide en x = 0 ; avec x=(l-lo) :

\overrightarrow{F}=-k.x.\overrightarrow{u_{x}}
La réaction tangentielle du support est constamment une force de frottement :

\overrightarrow{T}=-f.m.g.\overrightarrow{u_{x}}\quad si\quad\dot{x}>0

\overrightarrow{T}=f.m.g.\overrightarrow{u_{x}}\quad si\quad\dot{x}<0
Dans le cas d'un mouvement avec vitesse positive, x vérifie l'équation fournie précédemment :

\ddot{x}+\omega_{0}^{2}\cdot x=-f.g\quad avec\quad\omega_{0}=\sqrt{\frac{k}{m}}
La solution générale de cette équation est une somme de deux termes :
Une solution particulière correspondant au cas où la dérivée seconde par rapport au temps est nulle :

x_{p}=-\frac{f.g}{\omega_{O}^{2}}=-\frac{f.m.g}{k}
La solution de l'équation homogène c'est à dire de l'équation avec terme de droite nul :

x_{h}=K_{1}.\cos\left(\omega_{o}.t\right)+K_{2}.\sin\left(\omega_{o}.t\right)
On obtient donc :

x=K_{1}.\cos\left(\omega_{o}.t\right)+K_{2}.\sin\left(\omega_{o}.t\right)-\frac{f.m.g}{k} \\ \\ v=\dot{x}=\omega_{o}.\left[K_{2}.\cos\left(\omega_{o}.t\right)-K_{1}.\sin\left(\omega_{o}.t\right)\right]
Les conditions initiales définie précédemment permettent d'écrire :

-A=K_{1}-\frac{f.m.g}{k}\quad et\quad0=K_{2}
Au final :

x=-\left(A-\frac{f.m.g}{k}\right).\cos\left(\omega_{o}.t\right)-\frac{f.m.g}{k} \\ \\ v=\dot{x}=\omega_{o}.\left(A-\frac{f.m.g}{k}\right).\sin\left(\omega_{o}.t\right)
Je te laisse continuer...

Posté par
Tibozre : Méca : Ressort avec Frottement 26-10-18 à 14:45

Je pense avoir trouvé mais je demande confirmation...

L'énoncé me dit que le point M se met à glisser dans le sens des x décroissants, donc \dot{x} < 0 donc \vec{T} > 0

On a donc :
m\ddot{x} + k(x-l_{0}) = \parallel \vec{T}\parallel = R_{x}

avec :
x = x - l_{0} (car l_{0} = origine des abscisses)

On retrouve bien :
\omega _{0} = \sqrt{\frac{k}{m}}

et :
x_{eq} = \frac{fmg}{k}

Ensuite, on me demande de trouve l'abscisse x_{1} pour laquelle le point M s'arrête pour la première fois. On résout donc l'équa diff :

x(t) = x_{eq} + A\cos (w_{0}t) + B\sin (w_{0}t)

avec :
A = x(0) = x et B = \frac{\dot{x}(0)}{w_{0}}

Or : \dot{x}(0) = 0 donc B = 0

Donc :
x(t) = \frac{fmg}{k} + x\cos (\sqrt{\frac{k}{m}}t)

De plus :
\dot{x} = -x\sqrt{\frac{k}{m}}\sin (\sqrt{\frac{k}{m}}t)

Or : \dot{x} = 0 donc x = 0

Donc le point M s'arrête en x_{1} = \frac{fmg}{k}

Est-ce correct ?

Posté par
vanoisere : Méca : Ressort avec Frottement 26-10-18 à 18:34

Citation :
x = x - l_{0} (car l_{0} = origine des abscisses)

Cette formule n'a pas de sens ! Si l'origine des abscisses correspond au cas où le ressort a sa longueur à vide, il faut poser x= (l-lo) : exactement ce que je t'ai présentée précédemment.
Citation :
x_{eq} = \frac{fmg}{k}

Cela ne correspond pas à ce que tu as écrit sur ton brouillon. Il existe une infinité de positions d'équilibre possibles telles que :

|x_{eq}|\leq\frac{fmg}{k}
Si tu veux un mouvement dans le sens négatif à partir d'une position initiale avec vitesse initiale nulle, il faut choisir une abscisse initiale xo positive telle que :

x_{o}>\frac{fmg}{k}\quad avec\quad v_{o}=0
L'équation différentielle vérifiée par x tant que la vitesse reste négative est :

\ddot{x}+\omega_{0}^{2}\cdot x=f.g\quad avec\quad\omega_{0}=\sqrt{\frac{k}{m}}
Je te laisse la résoudre. Je t'ai indiqué la méthode dans mon précédent message

Posté par
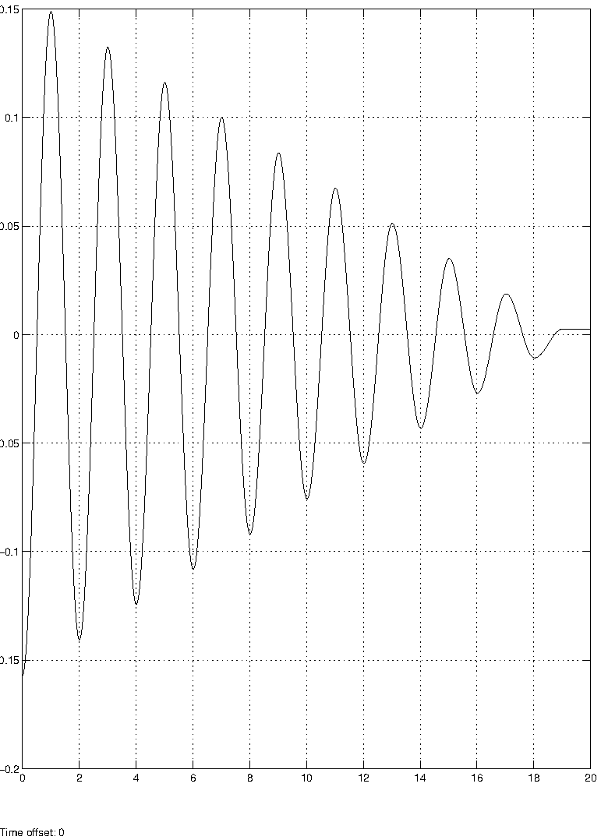
vanoisere : Méca : Ressort avec Frottement 26-10-18 à 20:20

Cela t'aidera peut-être un peu : voici une simulation avec une période propre de 2s. Tu vas y retrouver les caractéristiques du mouvement que j'ai décrites dans mon message du 24-10-18 à 19:44. J'en ajoute une autre. Le pendule s'immobile nécessairement au bout d'une durée multiple de la demie période propre pour une valeur de x telle que :

|x_{lim}|\leq\frac{fmg}{k}
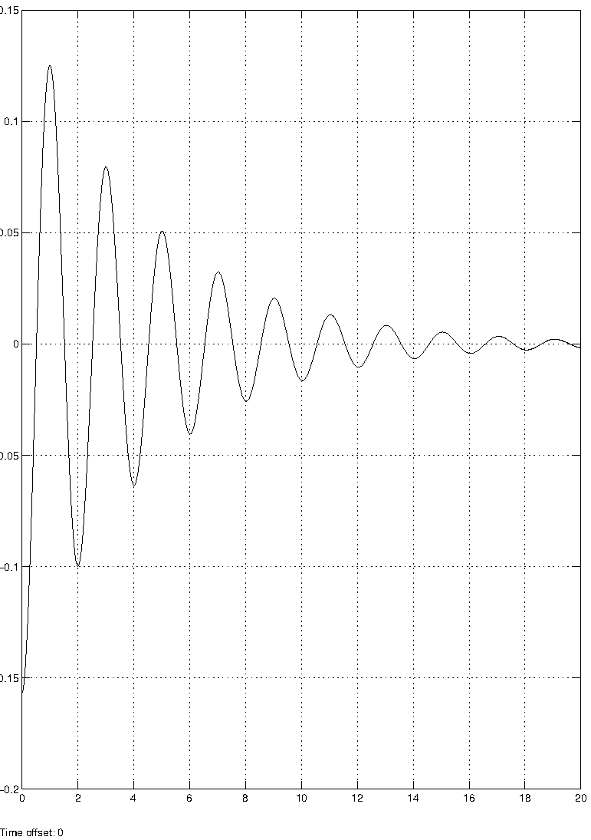
a titre de comparaison, j'ai posté en dessous le cas d'un oscillateur avec frottement fluide, les conditions initiales étant identiques.

Méca : Ressort avec Frottement

Méca : Ressort avec Frottement

Posté par
Tibozre : Méca : Ressort avec Frottement 29-10-18 à 12:52

Autant pour moi je reprends :

J'ai mon équa diff : \ddot{x} + \frac{k}{m}x = fg

Résolution avec les conditions initiales : position à t=0 ->x_{0} et vitesse initiale nulle (\dot{x}(0) = 0)

x(t) = \frac{fmg}{k} + x_{0}\cos (\sqrt{\frac{k}{m}}t)

Le point M s'annule pour la première fois quand sa vitesse sera nulle soit :
\dot{x} = 0 \Leftrightarrow -x_{0}\sqrt{\frac{k}{m}}\sin (\sqrt{\frac{k}{m}}t) = 0

Le seul terme pouvant varier est \sin (\sqrt{\frac{k}{m}}t), donc:

\sin (\sqrt{\frac{k}{m}}t) = 0 \Leftrightarrow \sin (\sqrt{\frac{k}{m}}t) = \sin (0)
\Leftrightarrow \sqrt{\frac{k}{m}}t = 0 + k\Pi (k\in N)
\Leftrightarrow t = 0 + k\Pi \sqrt{\frac{m}{k}} (k \in N)

DONC :

x(\Pi \sqrt{\frac{m}{k}}) = \frac{fmg}{k} + x_{0}\cos (\sqrt{\frac{k}{m}}\Pi \sqrt{\frac{m}{k}})
x(\Pi \sqrt{\frac{m}{k}}) = \frac{fmg}{k} + x_{0}\cos (\Pi )
x(\Pi \sqrt{\frac{m}{k}}) = \frac{fmg}{k} - x_{0}

Donc le point M s'annule pour la première fois en :

x_{1} = \frac{fmg}{k} - x_{0}

Est-ce correct ?

Posté par
vanoisere : Méca : Ressort avec Frottement 29-10-18 à 13:48

Du bon et du moins bon dans ce que tu as fait. Il faut que tu comprennes bien la méthode de résolution que j'ai exposée dans mon message du 25-10-18 à 23:20 même si  les conditions initiales que j'avais choisies arbitrairement ne sont pas celles que tu as précisées ultérieurement.
Tant que la vitesse reste négative, l'équa. diff. vérifiée par x est :

\ddot{x}+\omega_{0}^{2}\cdot x=f.g\quad avec\quad\omega_{0}=\sqrt{\frac{k}{m}}
C'est que tu as fait mais ensuite, il ne faut pas supposer a priori la constante égale à xo. La solution générale est de la forme :

x=K_{1}.\cos\left(\omega_{o}.t\right)+K_{2}.\sin\left(\omega_{o}.t\right)+\frac{f.m.g}{k} \\ \\ v=\dot{x}=\omega_{o}.\left[K_{2}.\cos\left(\omega_{o}.t\right)-K_{1}.\sin\left(\omega_{o}.t\right)\right]
Je te laisse vérifier que les conditions initiales conduisent à :

x=\left(x_{0}-\frac{f.m.g}{k}\right).\cos\left(\omega_{o}.t\right)+\frac{f.m.g}{k} \\ \\ v=\dot{x}=-\omega_{o}.\left(x_{0}-\frac{f.m.g}{k}\right).\sin\left(\omega_{o}.t\right)
Pour la suite, tu commets une maladresse : la lettre "k" désigne à la fois la constante de raideur du ressort et un entier relatif... De quoi s'y perdre ! Sinon, on constate effectivement que la plus petite valeur non nulle de t (notée t1) qui annule la vitesse vérifie :

\omega_{o}.t_{1}=\pi\quad;\quad t_{1}=\frac{\pi}{\omega_{0}}=\pi\cdot\sqrt{\frac{m}{k}}
soit une demie période propre.
la valeur correspondante de l'élongation est :

x_{1}=-\left(x_{0}-2\cdot\frac{f.m.g}{k}\right)
Si cette valeur vérifie : |x_{1}|>\frac{f.m.g}{k} , il ne s'agit pas d'une position d'équilibre possible ; le solide repart en sens inverse avec une vitesse positive...

Posté par
Tibozre : Méca : Ressort avec Frottement 30-10-18 à 11:02

Dans mon cours, on me donne, ce que tu appelles K_{1} et K_{2} définies comme cela :

K_{1} = x(0)
Donc K_{1} est définie par l'abscisse à t = 0, donc dans mon cas, c'est ce que je nomme x_{0}

K_{2} = \frac{\dot{x}(0)}{w_{0}}
Or comme, la vitesse à t = 0 est nulle, K_{2} est donc nulle

Donc il me reste que K_{1} = x_{0}

Je ne vois pas du tout comment tu fais pour trouver x=\left(x_{0}-\frac{f.m.g}{k}\right).\cos\left(\omega_{o}.t\right)+\frac{f.m.g}{k}

Posté par
vanoisere : Méca : Ressort avec Frottement 30-10-18 à 12:19

Ton cours concerne surement une équation différentielle de la forme :

\ddot{x}+\omega_{0}^{2}\cdot x=0  
Avec une constante non nulle, il faut utiliser la méthode que j'ai détaillée dans mon message du   25-10-18 à 23:20

Posté par
Tibozre : Méca : Ressort avec Frottement 30-10-18 à 13:08

C'est bon j'ai réussi à retrouver ta réponse vanoise !

Je dois maintenant trouver l'abscisse x_{2} à laquelle le point M s'annule pour la deuxième fois.

Je refais donc pareil sauf que je trouve une équa diff comme ceci :
\ddot{x} + w_{0}^{2}x = -fg

avec w_{0} = \sqrt{\frac{k}{m}}

Je trouve que la solution de cette équa diff est : x(t) = \frac{-fmg}{k} + (\frac{-fmg}{k} - x_{1})\cos (w_{0}t)

(Le point M repart de la position x_{1} à laquelle il s'était arrêté pour la première fois)

Et je trouve donc que le point M s'arrête pour la deuxième fois en :
x_{2} = -2\frac{fmg}{k} - x_{1}

Je peux ainsi généraliser les résultats précédents et dire que le point M oscille autour d'une valeur (qui serait l_{0} ? ) et ainsi tracer le premier graphe que tu as représenté plutôt ?

Posté par
vanoisere : Méca : Ressort avec Frottement 30-10-18 à 13:48

Absolument ! Attention : le graphe que j'ai tracé supposait une abscisse initiale négative et non positive). Tu devrais même pouvoir démontrer les propriétés essentielles d'un tel mouvement que j'ai rappelées dans mes messages du 24-10-18 à 19:44 et du   26-10-18 à 20:20.

Posté par
Tibozre : Méca : Ressort avec Frottement 30-10-18 à 14:11

Bien entendu, je pars d'une abscisse positive donc la courbe commencera à diminuer...
De plus, la pseudo-période reste identique en fonction du temps alors que l'amplitude diminue jusqu'à devenir nulle à un temps donné (quand l'abscisse sera comprise dans l'intervalle d'équilibre que j'avais calculé précédemment)

Posté par
vanoisere : Méca : Ressort avec Frottement 31-10-18 à 12:19

Je crois que tu as bien compris !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !