Inscription / Connexion Nouveau Sujet
MECA frottement (simple)
Bonjour,
J'ai un peu de mal à faire et comprendre les exercices de mécanique quand le frottement intervient...
J'aimerais savoir si vous pouvez m'aider 
c'est un exercice " simple " mais je ne sais pas comment le gérer:
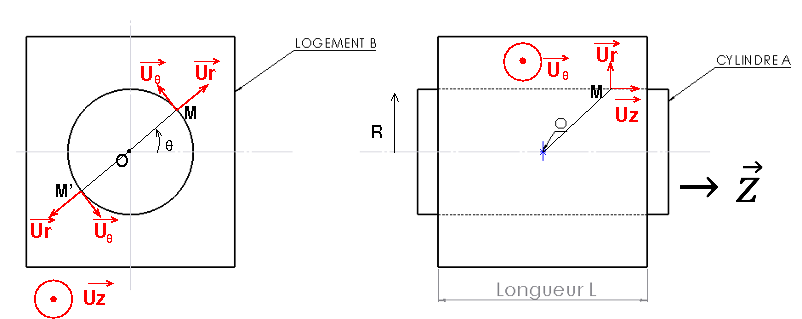
Un cylindre (A) se trouve dans son logement (B), la zone de contact est un morceau de cylindre ( rayon 'r' et longueur 'L' ). 'O' est au centre du trou et (O, [vecteur unitaire z]) et l'axe de symétrie de révolution. La contrainte est uniforme et le coefficient de frottement est également uniforme entre A et B.
1er cas : A est en translation par rapport à B
je doit trouver la les actions mécaniques de A sur B
// Dans le cas d'une translation parfaite je sais que la résultante est nulle (en faisant la sommes des efforts élémentaires ). Mais avec un coefficient t de frottement je ne sais pas si c'est le cas...
2em cas : A est en rotation par rapport à B. A tourne dans le sens positif de [[vecteur unitaire z]]
je recherche le torseur des actions mécaniques de A sur B
//F(A->B)= {[X Y Z] | [L M 0]} pour un base se terminant par z. mais je ne suis pas sur...
Merci de votre aide
Bonjour
Ce que tu as écrit n'est pas très clair !
Pourrais-tu scanner et poster le schéma fourni avec l'énoncé ? Pourrais-tu fournir l'énoncé intégral ?
merci de m'avoir répondu 
voici l'énoncé :
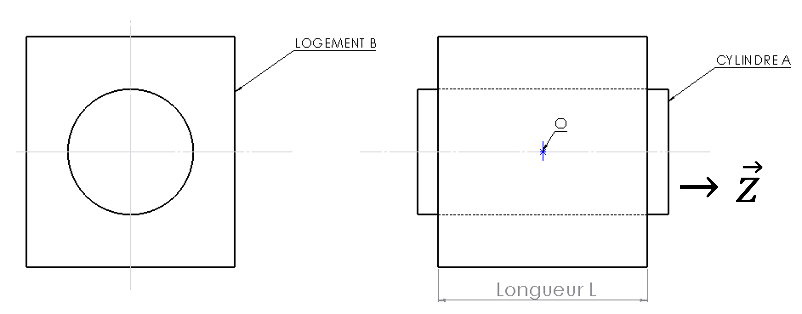
Un cylindre de révolution A est logé dans sont logement B. L'axe (O,z) est l'axe de symétrie de révolution.
La zone de contact entre A et B est un morceau de cylindre de longueur L et de rayon R.
La contrainte est normale uniforme sur la zone de contact entre A et B. Le coefficient de frottement entre A et B est également uniforme.
a) Si A est en translation vis-a-vis de B. Donnez la résultante des actions mécaniques de A sur B.
b) Si A est en rotation vis a vis de B. Donnez au point O, le torseur des actions mécaniques de A sur B. (A tourne dans le sens positive (orienté par z) vis à vis de B ).
Bonjour
Imagine un point M de la surface de contact entre le logement et le cylindre, ce point étant repéré par ses coordonnées cylindriques. Imagine une surface élémentaire du cylindre d'aire dS entourant le point M. Cet élément de surface exerce sur B une force radiale centrifuge proportionnelle à dS. Je note  la constante de proportionnalité :
la constante de proportionnalité :
Si A est en mouvement par rapport à B, l'élément de surface dS appartenant à A exerce sur B une force de frottement dont la norme est proportionnelle à la norme de dFN et qui est orientée suivant le sens et la direction du vecteur , le vecteur
étant le vecteur vitesse de glissement en M de A par rapport à B. La constante de proportionnalité entre les normes des deux vecteurs forces est le coefficient de frottement f : la force de frottement tangentielle à la surface a pour norme : dFT=f.dFN.
Cas où A est en translation par rapport à B : En tout point M, le vecteur vitesse de glissement est colinéaire à Uz :
La force de frottement exercée par l'élément de surface dS centrée en M sur B est donc de vecteur constant en tout point M de la surface de contact :
Ces vecteur forces élémentaires étant tous colinéaires et de même sens, la résultante des actions de A sur B est donc :
où S désigne l'aire de la surface de contact : S=2 R.L ; au final, la résultante est :
R.L ; au final, la résultante est :
Cas où A est en rotation par rapport à B : le vecteur vitesse de glissement en M de A par rapport à B est maintenant :
La force de frottement exercée par l'élément dS de A centré en M sur B s'écrit maintenant :
A tout point M de la surface de contact, on peut faire correspondre un symétrique M' par rapport à l'axe Oz. Les vecteurs U en M et en M' sont deux vecteurs opposés. Les vecteurs forces dF[sub]T[/sub] en M et en M' sont donc deux vecteurs forces opposés. Ce raisonnement étant valide pour tout point M de la surface de contact, on peut affirmer que la résultante de l'action de A sur B est le vecteur nulle. Le torseur de l'action de A sur B est donc un couple. Dans le cas d'un couple, le moment résultant est indépendant du point où on le calcule. Par commodité, on le calcule en O. Le moment élémentaire de la force dFT peut s'écrire :
en M et en M' sont deux vecteurs opposés. Les vecteurs forces dF[sub]T[/sub] en M et en M' sont donc deux vecteurs forces opposés. Ce raisonnement étant valide pour tout point M de la surface de contact, on peut affirmer que la résultante de l'action de A sur B est le vecteur nulle. Le torseur de l'action de A sur B est donc un couple. Dans le cas d'un couple, le moment résultant est indépendant du point où on le calcule. Par commodité, on le calcule en O. Le moment élémentaire de la force dFT peut s'écrire :
Le vecteur unitaire Ur en M et le vecteur unitaire Ur en M' sont deux vecteur opposés. On peut donc affirmé (même raisonnement que précédemment) que les composantes du moment du couple suivant Ur vont s'annuler deux à deux et donc avoir une somme égale au vecteur nulle. En revanche, les composantes suivant Uz vont s'ajouter ; le moment du couple correspondant à l'action de A sur B sera ainsi :
Je te laisse adapter les formules avec les notations de ton cours...
Merci de votre réponse 
je viens tout juste de trouver le même résultat que vous pour la question a). Pour cela j'ai décomposé les vecteurs résultantes et résolue cette intégrale (voir image). Pouvez vous me dire si l'écriture est correcte.
je vais étudier votre explication pour la b)
merci encore
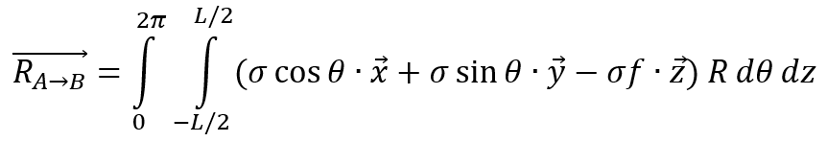
Cela conduit effectivement au même résultat puisque dS=Rd .dz et que le vecteur Ur a pour composante sur x : cos(
.dz et que le vecteur Ur a pour composante sur x : cos( ) et pour composante sur y : sin(
) et pour composante sur y : sin( )...
)...
Tu as choisi la méthode un peu calculatoire : cela fait plus de calcul intégral et de trigonométrie mais moins de réflexion ; au final : fais comme tu préfères. C'est d'ailleurs souvent comme cela que procèdent les professeurs de physique appliquée et de technologie...