Inscription / Connexion Nouveau Sujet
Meca complexe
 philou28
philou28Bonjour à tous
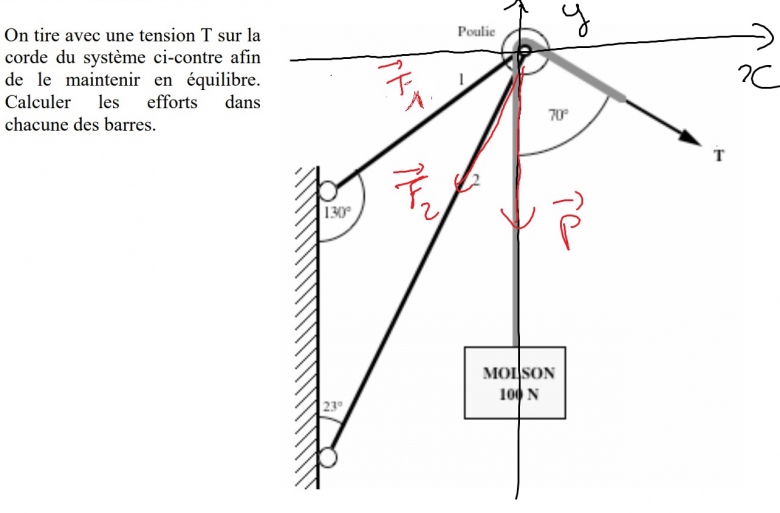
J'ai un exercice à résoudre mais je suis bloqué, j'applique le PFS sur la poulie et il y a trop d'inconnue :
Tsin70 + F1cos 40 - F2sin23 = 0
-100 + Tcos70 - F1sin40 - F2cos23 = 0
Si quelqu'un à des idées...
Merci beaucoup
Bonjour
Tu oublies les propriétés de la poulie qui ici ne tourne pas alors qu'elle est mobile en rotation sans frottement.
D'autre part, le sens d'une des forces est irréaliste : tu ne peux pas envisager un équilibre avec la totalité des forces ayant une composante suivant y négative !
Autre chose : ne pas mélanger dans une même formule valeurs littérales et valeurs numériques.
Merci pour votre réponse
Ce problème vient du Quebec et ne sera pas corrigé, il n'y a que la valeur numérique des forces comme correction. Je vais au plus vite car il y en a beaucoup.
Je ne vois pas comment représenter les forces.
Je ne peux donc pas appliquer le PFS ?
Merci
En supposant la poulie mobile en rotation sans frottement et en supposant le câble de masse négligeable, tu peux considérer la poulie comme un simple transmetteur d'effort. Les forces de vecteurs et
ont ainsi la même intensité. Tu as donc un problème à deux inconnues : les intensités des forces
et
. Tu obtiens un système de deux équations en projetant le PFS sur les deux axes. Deux équations pour deux inconnues : le compte est bon !
Attention aux sens des forces : si la barre n° 1 travaille en tension, la barre n° 2 travaille en compression. Pour obtenir une somme vectorielle nulle, les composantes des quatre vecteurs suivant chaque axe ne doivent pas toutes être de même signe !
Il te faut donc revoir ta figure et les relations de projection du PFS.
Merci
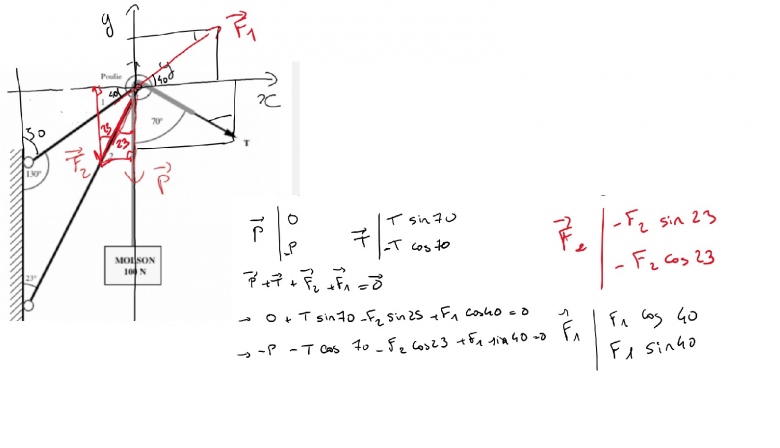
Voila ce que j'ai fait mais en résolvant ce système je n'ai pas encore les bonnes réponses ( ils trouvent : 306 et -359 N
Ai je fait encore une erreur ?
Revenons aux bases...
Le système à l'équilibre dans le repère terrestre galiléen est la poulie, considérée de masse négligeable (on peut négliger son poids ici). Les forces prises en compte sont les forces extérieures c'est à dire les forces exercées sur la poulie par le milieu extérieur. En particulier, les forces exercées sur la poulie par les deux barres.
Imagine par exemple que la barre n° 1 se casse : que se passerait-il ?
Imagine par exemple que la barre n° 2 se casse : que se passerait-il ?
Il te faut revoir les sens de ces deux forces.
PS : selon le règlement du forum : tu dois scanner le schéma mais il te faut copier ta solution dans l'éditeur de texte.
Bonjour,
Une remarque : le système du message de @philou28 12-09-24 à 23:15 donne bien les bonnes valeurs.
C'est-à-dire -306 N et -359 N avec vos orientations qui doivent être différentes de celles du corrigé.
Quand je regarde tes projections de forces, T ,P ,F1, F2 désignent les intensités des forces, c'est à dire les normes des vecteurs forces. Tu dois donc obtenir des valeurs strictement positives. Si tu obtiens une valeur négative, c'est qu'il y a un problème de sens de vecteur force.
le système du message de @philou28 12-09-24 à 23:15 donne bien les bonnes valeurs.
Pour moi, une bonne réponse en ce qui concerne un vecteur doit concerner la direction, le sens et la norme.
Imagine que tu casses la tige n° 1 , les autres forces étant maintenues : la poulie s'éloignerait du mur. Pour empêcher cela,
Imagine que tu casses la tige n°2, les autres forces étant maintenues. La poulie descendrait. Pour empêcher cela,
Bref : il te faut reprendre ta première figure du 12-09-24 à 19:43 en inversant le sens de
gts2 : je trouve en résolvant le système : -376 et -330 N
Vanoise : moi cela me dérange beaucoup mais sur le cours du professeur du Quebec le - ne le dérange pas.
Donc en suivant les conseil de vanoise je trouve 376 et 330 N, c'est différent du corrigé.
Mes angles vous semblent correct ?
En France, les normes des vecteurs force que l'on note indifféremment ou F sont obligatoirement des valeurs positives qui correspondent pratiquement aux intensités des forces, on dit parfois "valeurs" des forces. En revanche, les composantes des vecteurs dans un repère donné, qui peuvent être notées Fx et Fy peuvent être positives ou négatives en fonction du sens des vecteurs et du repère choisi.
Le plus important pour juger de la compréhension physique du problème est le schéma où figurent clairement les directions et les sens des vecteurs force. Tu as eu un problème à cet égard.
En modifiant le sens de l'action de la barre n° 2 comme indiqué dans mon dernier message, on obtient le système suivant :
-F1.cos(40)+F2.sin(23)+T.sin(70)=0
-P-F1.sin(40)+F2.cos(23)-T.cos(70)=0
avec : P=T=100N.
Cela me conduit, en arrondissant à trois chiffres significatifs, à :
F1=306N ; F2=359N.


