Inscription / Connexion Nouveau Sujet
Masse totale
Bonsoir,
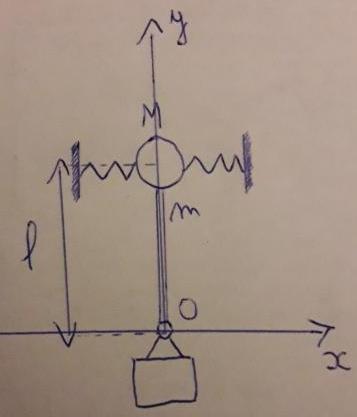
Un pendule astatique: tige rigide de longueur l et de masse m relié à une masse M, elle-même intercalée entre 2 ressorts de raideur k. On négligera les masses des ressorts.
Je cherche la masse totale et sur la correction, il y a marqué M + (m/3). Mais je ne comprends pas ce résultat, faut t'il diviser la masse de la tige par 3 parce qu'elle pend 2 ressorts et une masse ?
Bonsoir
Et si tu postais le schéma du dispositif et si possible un énoncé complet ? Il est possible que l'application du théorème du moment cinétique au solide constitué de la masse M et de la tige fasse intervenir (M+m/3) dans l'expression de la période.
Déterminer la période des petites oscillations du système suivant : (schéma) et après il y a marqué ce que j'ai marqué en haut.
Sur la correction avec la loi de conservation de l'énergie, il y a marqué:
E=T+U=([M+(m/3)]/2)(dx/dt)^2+ expression de U. J'en ai donc déduis que la masse totale est M+ (m/3)
On peut aussi raisonner sur la conservation de l'énergie mécanique.
Tu as un solide en rotation autour d'un axe fixe. Tu connais sûrement l'expression de l'énergie cinétique en fonction du moment d'inertie et de la vitesse angulaire.
Attention : la masse totale du système est évidemment (M+m). C'est en simplifiant l'expression de la période qu'apparaît un terme en (M+m/3) comme déjà expliqué !
Je ne sais pas comment appliquer le théorème de Huygens-Steiner pour trouver le moment d'inertie afin de déterminer l'énergie cinétique sachant que I(tige)=Ml²/12.
C'est le moment d'inertie de M= moment d'inertie de m ?
Le moment d'inertie d'une tige homogène de masse m, de longueur l, par rapport à un axe qui lui est perpendiculaire et passe par une de ses extrémités est . Le moment d'inertie de la masse M considérée comme quasi ponctuelle et située à la distance l de l'axe de rotation est
.
L'énergie cinétique d'un solide en rotation autour d'un axe fixe  est :
est : . Pour le solide de masse (M+m) l'énergie cinétique a pour expression :
Or, pour des oscillations de faible amplitude : ; on retrouve bien l'expression de ton corrigé !
Comment trouver I(tige)=ml²/3 ?
Moi je fais(pour une tige de masse m et de longueur l, sur l'axe x): I1=0, I2=I3= l/2-l2 P (x²) dx avec P masse linéique =m/l et l'intégrale donne l3/12 donc ça donne ml²/12
l/2-l2 P (x²) dx avec P masse linéique =m/l et l'intégrale donne l3/12 donc ça donne ml²/12
Je note µ ma masse linéique de la tige homogène de longueur l telle que m=µ.l. Je choisis l'origine O de mon repère à une extrémité.
Ah oui c'est vrai ! J'avais placé l'origine au milieu de la tige. Maintenant c'est clair, merci bien.
Bonjour, je ne comprends pas très bien la différence entre ce pendule astatique et un pendule simple.
Nous utilisons l'énergie cinétique d'un solide parce que la tige a une masse m et donc n'est pas négligée devant la masse de la masse M comme pour le pendule simple ?
Tu as un oscillateur harmonique, c'est à dire un oscillateur conduisant à des oscillations sinusoïdales en absence de frottement à chaque fois que l'énergie potentielle est proportionnelle au carré de l'élongation (cas d'une translation) ou au carré de l'élongation angulaire (cas d'une rotation).
Pour ce pendule astatique, il s'agit de l'énergie potentielle élastique des deux ressorts et de l'énergie potentielle de pesanteur qui à pour expression : en cas d'oscillations de faible amplitude. L'expression est de la même forme pour un pendule dans le cas d'oscillations de faible amplitude mais la constante K est différente et ne prends en compte que l'énergie potentielle de pesanteur.
Dans le cas du pendule, deux études sont possibles :
1° : le pendule simple : masse quasi ponctuelle et fil inextensible de masse négligeable.
2° : le pendule composé assimilé à un solide en rotation : on peut tenir compte des dimensions du solide en rotation, on peut tenir compte de la masse et du moment d'inertie de la tige de liaison... plusieurs modélisations plus ou moins proches de la réalité sont envisageables. Dans tous les cas, la période propre des oscillations de faible amplitude peut s'écrire :
avec :
I( ) : moment d'inertie par rapport à l'axe de rotation
) : moment d'inertie par rapport à l'axe de rotation
M : masse totale du pendule
a : distance entre l'axe de rotation et le moment d'inertie du pendule.