Inscription / Connexion Nouveau Sujet
Masse m suspendu à un fil
Bonsoir,
En travaillant des exercices de dynamique, je me suis trouvé incapable de choisir la " bonne " base.
Un point matériel de masse m est suspendu en un point O fixe par un fil inextensible, de longueur L et de masse négligeable. Ce point décrit un cercle de rayon r à la vitesse angulaire constante , et l'angle que fait le fil avec la verticale est noté
1) Calculer la tension T dul fil en fonction de m, et L.
2) Calculer la valeur de et montrer q'une valeur minimale
est nécessaire pour que ce pendule conique puisse fonctionner.
J'ai essayé d'utiliser une base polaire, mais je n'arrive à aucune conclusion logique. Je trouve que la vitesse est nulle ( car l'angle alpha est constant ) . Je ne comprend pas aussi le choix du repère (O,x,y,z), et si on a le droit de dire que dans un mouvement circulaire l'accélération est centripète sans le démontrer.
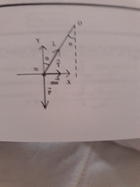
J'ai attaché une image du schèma de l'exercice.
J'espère que vous puissiez m'aider afin d'assimiler mon cours et d'améliorer ma capacité à choisir une bonne base, un bon repère.
Merci d'avance !
Voici l'image, je m'excuse du double post , je n'ai pas remarqué dans le message précédent qu'elle n'a pas été envoyé.
Bonjour
Comme le précise l'énoncé, il s'agit d'un pendule conique. La masse m et le fil tournent à la vitesse angulaire 
autour d'un axe vertical fixe passant par O, le fil se déplaçant ainsi sur un cône de sommet O . Comme indiqué sur ton schéma, l'accélération de la masse par rapport à la terre est une accélération normale centripète... Je te laisse continuer !
.Je vous remercie pour vos réponses vanoise et gbm .
Les liens proposés m'ont été forts utiles.
Veuillez m'excuser, mais en prenant (M,,
,
) , on trouve
, donc
et puisque alpha est constant, on trouve la vitesse est égale au vecteur nul, non ?
Merci d'avance !
Tu raisonnes comme si tu avais un pendule simple, la masse et le fil oscillant dans un plan vertical fixe !
Imagine au contraire 
fixe, le pendule tournant autour de l'axe vertical passant par O (la verticale en pointillé de ton schéma) :
La masse ponctuelle décrit un cercle dans un plan horizontal dont le centre est le point H, projeté orthogonal de la masse m sur la verticale déjà évoquée. Le rayon de la trajectoire est ainsi : r = L.sin().
A toi de déterminer l'accélération puis d'appliquer la seconde loi de Newton (PFD)...
Annuler
connectez vous