Inscription / Connexion Nouveau Sujet
masse et équilibre mécanique
Bonjour à tous,
J'ai un problème que je n'arrive pas à résoudre, voici l'énoncé:
Un bloc B de masse 72kg est posé sur une table, le coefficient de frottement de la table vaut u= 0.25 = f/R av f:force de frottement et R: la réaction du support. On suppose que la corde reste horizontale.
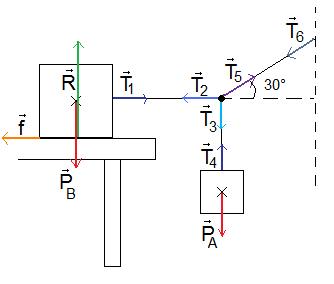
Question : déterminer la masse maximale du bloc A telle que le système reste à l'équilibre.
En fait je ne sait pas vraiment par quoi commencer:
Je pense qu'il faut étudier le système à l'équilibre, puis appliquer le PFD
Mais par quel solide commencer? Je pense que le B serais le premier, mais pour la suite j'ai un doute, faut il appliquer le PFD au nœud ou d'abord au solide A?
Et pour la force de frottement sa valeur est égale à : f/R ou - u.v av v la vitesse et u le coef de frottement?
merci à tous
D'après le schéma, il est évident que la composante verticale de la tension du fil relié au plan de droite compense nécessairement le poids du solide A.
L'angle que forme ce fil avec l'horizontale implique que la tension possède une composante horizontale, proportionnelle à la composante verticale, et qui ne peut être compensée que par la tension du fil relié au solide B.
Cette dernière tension étant elle même compensée par le frottement entre le solide et la table.
Il me semble qu'il y a là toutes les relations nécessaires.
Il reste à comparer à la valeur maximale que peut prendre , conditionnée par l'inégalité:
Je ne suis pas sur de tous comprendre
En fait d'après toi (et si j'ai bien compris), on a les relations suivantes:
PA = T4 car le poids est compensé par le fil,
de la même manière:
T5 = T6
T1 = T2
Si les relation ci dessus sont exactes, je pourrais appliquer le PFD au solide B pour trouver T1, appliquer le PFD au solide A en fonction de sa masse, mais comment puis-je avoir T6?
Et puis dois-je appliquer le PFD ou dire qu'à l'équilibre,
 Fext = 0 ??
Fext = 0 ??
Ce que je suggérais était directement d'écrire que:
et d'utiliser le fait que le rapport des composantes du vecteur tension vaut d'après le schéma .
Je ne pense pas que tu aies besoin de détailler l'ensemble des forces intermédiaires pour le voir, si? (à moins qu'on te l'impose bien entendu)
je ne comprends pas ta notation pour le vecteur T5
mais dans mon cours je n'est que la solution du PFD à appliquer donc
en résumé pour que l'ensemble reste à l'équilibre, il faut que:
T1 = PB + R + f
et
T3 = T4 = PA
et
T5 = T6 = ??
ensuite on pose :
T1 + T3 + T5 = 0 en fonction de mA puis on résous? Non?
Mais T5 m'est toujours inconnu
Si sa n'engage que moi,
on aurai:
T5 = T1 + T3 comme nous sommes à l'équilibre.
Mais est ce que tous le raisonnement précédent est correct?
Car si j'applique le PFD
* au solide B, on a:
PB + R + f + T1 = 0
=> f + T1 = 0
=> u (coef de frott) * v = T1
mais ici, le solide reste immobil donc v=0 => T1=0 imposssible???
*au solide A, on a:
PA+ T4 = 0
=> PA = T4
=> mA.g = T4 = T3
au noeud on a:
T1 + T3 + T5 = 0
En fait la dedans ce qui me dérange le plus, c'est les axes de projections je ne sait pas comment les placer beaucoup de vecteurs forces sont orthogonaux
ha non je vien de comprendre le raisonnement en relisant ton premier topic!
merci beaucoup pour ton aide
Si tu le dis... 
J'espère seulement que tu as réalisé que le coefficient de frottement donné relie la composantes normale de la réaction du support à la composante tangentielle (i.e. les frottements) mais en aucun cas ne relie cette dernière à la vitesse.


