Bonsoir
Que cherches tu exactement  ?
À établir l'expression de l'abscisse x(t) d'une masse de la machine d'Atwood  en tenant compte de la masse lineique du câble  ? Cela se fait assez bien en considérant qu'en absence de frottement, l'énergie mécanique de la machine d'Atwood est la même à une date t et à la date (t+dt ).

A vrai dire j'aimerais arriver a la formule qu'ils décrivent a savoir l=l0 ch( g/l )*t

C'est bien ce que je te proposes de faire. Il faut t'aider de schémas pour bien comprendre ce que désignent l et l_o et x. Attention au placement des parenthèses dans tes formules. Revois si nécessaire ton cours de math sur le cosinus hyperbolique, autrefois noté "ch". Maintenant on écrit de préférence  :

Oups desolé tout cela est un peu nouveau pour moi 😅. Du coup après quelques vidéos sur le sujet il semble que l'équation finale ait un lien avec le principe de chainette.
Et d'après ce que j'ai compris on a l qui correspond a la longueur de la portion de chainette entre le point le plus bas et le point d'encrage de la chainette.

x correspondrait a la flèche soit  la distance entre les deux points d'accroche et le point le plus bas de la chaine.
Par contre j'ai un peu de mal avec la notion de l0. Je suppose que la longueur x est égale a la portion de chaine l a un instant t.
Pour l'instant est-ce correct ?

Ton énoncé n'est pas très rigoureux et c'est en examinant les résultats obtenus que je pense avoir "deviné" le dispositif capable de conduire à ces résultats...
Le dispositif n'est pas à proprement parler une machine d'Atwood (voir exemple de machine d'Atwood ici par exemple : )
Il s'agit simplement d'une chaînette de masse linéique µ, de diamètre négligeable, enroulée régulièrement sur une poulie de rayon très grand devant le diamètre de la chaînette. La longueur totale de la chaînette est "l".
Une portion de longueur lo de la chaînette pend verticalement et le dispositif est maintenue sans vitesse initiale. A la date t= 0, on abandonne le système à lui-même sans vitesse initiale. Sous l'action du poids de la partie verticale du fil, la poulie se met en rotation et la chaînette se déroule. On note x=f(t) la longueur de la partie verticale de la chaînette.
En utilisant la conservation de l'énergie comme expliqué dans mes précédents messages et en négligeant l'énergie cinétique de la poulie en rotation, il faut commencer par établir l'équation différentielle vérifiée par x= f(t). Le résultat est fourni par l'énoncé :


Il faut ensuite chercher à résoudre cette équation différentielle du second ordre. Il faut chercher des solution de la forme :
x=K.e^r.t
où r est solution de l'équation caractéristique... Revois au besoin ton cours de math.
En tenant compte des conditions initiales, tu devrait arriver à :

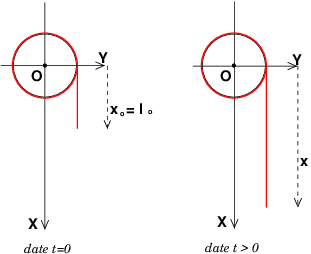
Bonjour Vanoise, bonjour Gimlix,

J'avoue que cette equa. diff. m'a aussi intrigué et j'en étais arrivé là (cf croquis) je pense que c'est bon aussi, en négligeant les frottements.
Mais c'est pas une machine d'Atwood non plus

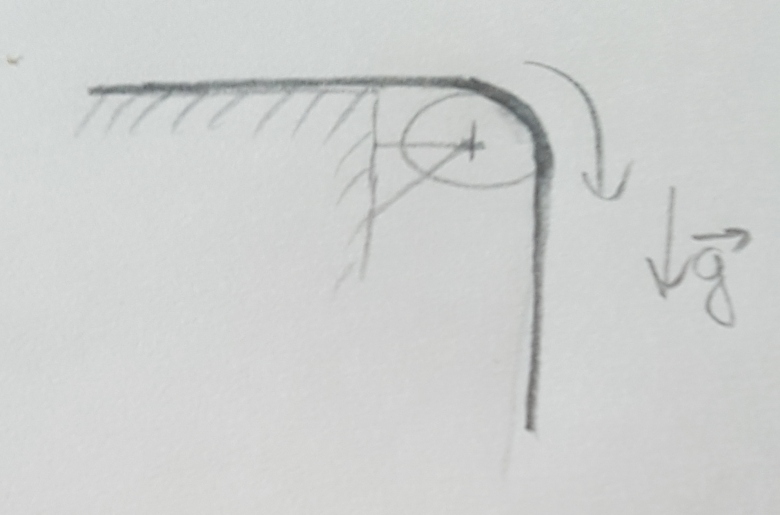
Bonjour krinn
Effectivement, ton dispositif aboutit à la même équation différentielle.  
Je ne comprends pas tous ces concepteurs d'énoncé qui ne fournissent pas de schéma du dispositif étudié...

Bonsoir,
Alors merci de vos réponses. Du coup en posant a=d²x/dt²=(g/l)x
J'ai x''(t)- (g/l) (t)=0. En admettant que l=1 et que j'ai
Et pour l'instant ça me donne r1=Ke^3,13x. Je ne sais pas si c'est juste j'ai essayé de compenser avec mes anciens cours mais c'est assez difficile 😅.

Cette méthode consistant à mélanger valeur numériques et valeurs littérales conduit à n'importe quoi.
On cherche une solution de la forme : . Je te laisse démontrer :



On reporte dans l'équation différentielle :



puisque x>lo , on peut diviser par x l'égalité précédente. On obtient l'équation caractéristique :

qui admet deux solutions réelles :



L'expression générale de x est ainsi de la forme :



Reste à trouver les constantes K1 et K2 à partir des conditions initiales. Tu pourras alors constater que le résultat est équivalent à :



Je crois que tu aurais grandement intérêt à revoir ton cours de math sur les équations différentielles...

Bonsoir

Tu peux réviser ce type d' equa. diff. avec ce lien:


Ce qui serait interessant, c'est que tu postes la figure du livre où est définie la "machine d'Atwood" en question, car pour une (vraie) machine d'Atwood, l'accélération n'est pas celle qui est indiquée !

Bon, j'ai refait tout le cheminement de vanoise. J'obtiens bien que la d²x/dt²=r²x. J'obtiens aussi la meme équation a 2 constantes. Par rapport aux conditions initiales on sait qu'a l'instant initial x₀=l₀. Ainsi si on remplace "t" par 0 dans l'équation, on obtiens K1+K2=l₀.

On sait aussi que cosh= (e^x+e^-x)/2 comme dans notre cas . Finalement on a
x(t)=2cosh( √(g/l)×t)×l0. Voilà je ne vois pas comment me débarasser de ce facteur 2.

Tu viens de calculer la somme (K1+K2). Très bien mais tu n'as pas déterminé la valeur de K1 et la valeur de K2.  Pour cela il faut en plus écrire que la vitesse dx/dt est nulle si t=0.

Honnêtement je ne vois pas comment obtenir les conditions initiales. Je veux dire qu'elles ne sont pas énoncées du type y(0)=1 et y'(a)=... .  je ne vois vraiment pas comment sans ces conditions on peut avoir K1 et K2

x=K1.e^r1.t + K2.e^r2.t
Tu peux dériver par rapport à t  pour obtenir la vitesse puis écrire que cette vitesse est nulle si t=0. Cela va te donner une deuxième relation entre K1 et K2. Avec celle que tu as déjà obtenue, cela te donne un système de deux équations pour deux inconnues : K1 et K2.

Je pense avoir trouvé !
Alors on pose K1+K2=l₀ donc K1=l₀.
Aussi on a en deuxième equation:
x'=K1×r1+K2×r2 si t=0.
Donc si on remplace on a :
(l₀-K2)×r1+K2×r2=0
r1×l₀-K2×r1+K2×r2=0
Si on considère que r1=-r2 alors on peut remplacer et simplifier ce qui nous donne :
x'=l₀-2K2=0.
Donc K2=l₀/2 de même que K1.
Ainsi si on remplace on a dans la dernière équation : x=(l₀/2)×e^r1.t + (l₀/2)×e^r2.t
On met l₀/2 en facteur :
l₀ (e^r1.t + e^r2.t)
=(l₀/2)*2 cosh (r1.t)
On simplifie les 2 et cela semble correspondre. Est ce correct ?

Oups erreur de ma part a la première ligne K1=l₀-K2

Parfois un peu maladroit comme démonstration mais tu as trouvé l'essentiel :


D'où l'expression de x(t). Pour conclure et trouver la durée t_f nécessaire pour que toute la corde se déroule et quitte la poulie, il suffit d'écrire :

t=t_f si x=l.

Très bien, merci beaucoup a vous pour m'avoir suivi jusqu'au bout. Bonne soirée