Inscription / Connexion Nouveau Sujet
Machine d'atwood
Bonjour,
Je suis sensé faire un problème de physique mais je n'y arrive pas ! La machine d'atwood simple je la comprend comme ma poche mais voila une version plus compliqué et je demande donc votre aide.
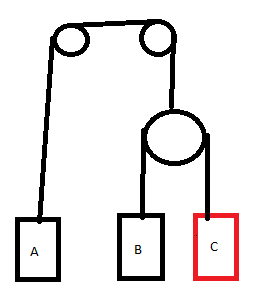
On considère le système de la figure.
Les poulies sont considérées sans frottement et de masse négligeable.
a ) Montrez que Aa = -( Aa + Ac) / 2, ou Aa,ab et Ac sont les accélérations verticales des masses A,B,C
b ) Donnez la relation entre les tensions des deux câbles
c) Ecrire pour chacune des masses la 2ème loi de Newton
d ) En utilisant a) b) c), déterminez alors l'accélération de la masse A en fonction des masses , Ma,
Mb, Mc et de g.
e) Application numérique:
Ma = 5 kg, Mb = 3 kg, Mc = 2 kg.
Bonsoir,
Au point C et D.
Je n'arrive pas à séparer des accélérations pour en trouver une formule ne comportant que des masses et G.
C)
Vecteur : Ta = Tbc
Tb' + Tc' + Tbc = 0
Ta = Tb + Tc
D)
-gMa + Ta = Ma * Aa
-gMb + Tb = Mb * Ab
-gMc + Tc = Ma * Aa
il n'y a qu'une tension par câble!
qu'on peut noter T1 pour le câble attaché à A
et T2 pour le câble BC
et comme on néglige la masse des poulies T1 = 2T2
tu as 5 inconnues: 
A B C T1 T2 et tu as 5 relations
donc tu dois y arriver!
je ne vois pas ou tu veux en venir.
Je me trouve avec un système de 3 équations et 5 inconnu ! ou trouver les 2 manquantes ?
celle du points a) mais il m'en manque une.
b ) Donnez la relation entre les tensions des deux câbles
j'isole la poulie à laquelle sont pendus B et C
elle subit une force T1 vers le haut et deux fois la force T2 vers le bas (une fois vers B et une fois vers C)
elle n'a pas de masse donc
T1 - 2 T2 = 0
T1 = 2 T2
je ne vois pas ce que tu appelles Tbc
Tbc pour moi c'était Tb + Tc
Alors je suis alors avec un système de 3 équations
-Ma g + 2T2 = ma + aa
-Mb g + T2 = mb + ab
-Mc g + T2 = mc + ac
et l'équation dans le point a)
ça fait 4 équation et 4 inconnues, je vais essayer de voir si je réussi à développer ça
J'ai pas réussi. Équation trop grande je suis sûr d'avoir fait des erreurs quelque part.
et je me suis trompé dans ce que j'ai écrit en dessus ct Mx * Ax pas +.
pourtant tu y es presque:
ma a = T1 - ma g
mb b = T2 - mb g
mc c = T2 - mc g
b + c = -2 a
T1 = 2 T2
5 éq., 5 inconnues, et on cherche a
b = T 2/mb - g
c = T 2/mc - g
donc b + c = T2 (1/mb + 1/mc) - 2g
= (mb + mc)/(mb mc) T2 - 2g
comme
b + c = -2 a
on a:
(mb + mc)/(mb mc) T2 - 2g = -2 a
T2 = 2 
(g - a ) en posant = (mb mc) / (mb + mc) (masse réduite de B et C)
on reporte tout ça dans la 1ère éq.
ma a = T1 - ma g
sachant que T1 = 2T2
on trouve finalement:
a = (4 - ma)/(4 + ma) g
sauf erreur (car il est tard 
Annuler
connectez vous