Bonjour
On t'a déjà demandé de renseigner ton profil (niveau d'études), ce que tu n'as pas fait.
Dans cette attente, ton sujet est verrouillé.
Lorsque tu auras renseigné ton profil, tu peux utiliser "signaler un problème" en bas de page, pour pouvoir poster à nouveau.


**situation régularisée**

Bonjour
As-tu bien compris le principe du coin  de verre ? La source de lumière monochromatique étant une source étendue : où se trouvent localisées les franges ? Comment sont-elles positionnées par rapport au coin de verre ?
Je pense qu'un schéma clair que tu pourrais scanner et poster ici rendrait l'aide plus facile.
Ensuite, pour répondre à la question posée, il faut déterminer l'expression de l'interfrange i.

Bonjour Vanoise.
Le fait est qu'on nous a présenté cet exercice mais ne nous avons donné rien à propos de cette notion ( coin de verre). J'ai essayé de faire des recherches là dessus mais je n'ai pas pu trouver d'explications précis à propos...

Le coin de verre est un prisme en verre dont l'arête est perpendiculaire au plan de figure, sa trace dans le plan de figure étant le sommet O. On parle de "coin" seulement si, comme c'est le cas ici, l'angle au sommet du prisme est extrêmement petit. Comme je vais le montrer, le phénomène d'interférence  se produit entre deux faisceaux obtenus par réflexion partielle de la lumière sur les dioptres. Or, sous incidence normale ou quasi normale comme ici, un dioptre ne réfléchit qu'environ 4% de l'intensité lumineuse, les 96% étant transmis par réfraction. Pour que cette lumière transmise par réfraction ne vienne pas "éblouir" l'observateur et empêcher l'observation du phénomène d'interférence, on la dévie grâce à une lame semi transparente qui à la propriété de transmettre 50% de l'intensité lumineuse incidente et d'en réfléchir 50%.
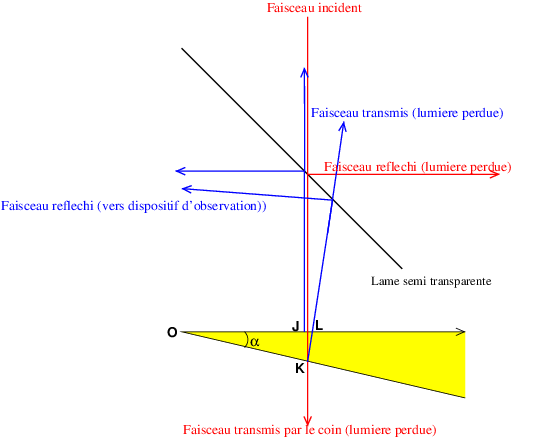
J'ai tracé ci-dessous la marche d'un rayon incident du faisceau incident normal à la première face du coin. 50% de l'intensité lumineuse est réfléchie vers la droite du schéma et perdue pour l'expérience. 50% de l'intensité est transmise jusqu'en J :
4% de cette intensité est alors réfléchie en sens inverse vers la lame semi transparente qui en réfléchi la moitié vers la gauche (dispositif d'observation). J'ai décalé légèrement sur le schéma, pour plus de clarté le rayon incident en route et le rayon réfléchi en bleu. Les 96% de la lumière réfractée en J continuent jusqu'à K et 4% de l'intensité en K est réfléchie jusqu'en L en direction de la lame semi transparente. Le reste est réfractée en K et perdue pour l'observateur. Il y a donc interférence entre l'onde lumineuse réfléchie en J et l'onde lumineuse réfléchie en K.
Je te laisse calculer la différence de marche entre ces deux ondes. Sa chant que la valeur de est très faible,et que l'incidence est quasi normale, lla différence de marche est pratiquement égale au double de la distance JK, les points J et L étant quasi confondus. Facile alors d'exprimer cette distance JK en fonction de et de x=OJ. Il faut alors trouver les valeurs de x qui correspondent à des maximum d'intensité lumineuse (milieux des franches claires) et en déduire l'interfrange i.
Je te laisse aussi réfléchir à la localisation des franges. Tu peux aussi vérifier que les intensités des deux ondes qui interfèrent sont très proches, ce qui permet une bonne visibilité des franges (bon contraste entre maximums et minimums d'intensité lumineuse).

Merci monsieur pour tous ces détails.
Par la définition de l'interfrange, j'ai trouvé i= lambda/2alpha mais pour la suite je n'arrive pas.

Pour une distance "d" mesuré sur l'axe perpendiculaire aux franges, le nombre moyen de franges de même nature (brillante ou sombre) est N_moyen = d/i.
Maintenant, il faut réfléchir au nombre réels de franges de même nature ( un nombre entier nécessairement) que l'on peut obtenir entre deux repères distants de d=1mm...

Monsieur, je pense que le nombre réel de franges de même nature est la partie entière de N _moyen mais je n'arrive par à déterminer N _moyen dépendant de dont la valeur n'a pas été donnée.

D'accord monsieur. J'ai donc trouvé i=3mm. Mais je pense que la valeur de d serait plutôt 1cm car l'exercice demande le nombre de franges d'interférence par centimètre. Du coup, j'ai trouvé égal 3,33 soit 3 franges d'interférence par centimètre.

D'accord avec toi !
Tu pourrais me rappeler l'expression littérale de la différence de marche ? Il y a un (petit) piège qui n'intervient pas pour cette question mais qui pourrait conduire à une réponse erronée à une question de ce type :
" quelle est la nature de la frange centrée en x= OJ=3i ? " ...

La différence de marche a pour expression =2x. L'ordre d'interférence sera donc p=2x/.

De l'expression de i, on peut dire que p=x/i. Lorsque x=3i, p= 3. Donc il s'agit d'une frange brillante.

J'ai bien fait de poser cette question complémentaire !
En effet, contrairement à la réflexion sur un dioptre verre - air (réflexion en K), la réflexion sur un dioptre air-verre produit une inversion de signe du signal lumineux. Cette inversion de signe est équivalente à un déphasage supplémentaire de radians, ce qui est équivalent à une différence de marche supplémentaire de /2 par rapport à la différence de marche géométrique calculée par ailleurs. La différence de marche équivalente pour le calcul de l'intensité lumineuse ou pour l'étude de la nature des frange est donc ici  :
=2..x+/2
Je te laisse vérifier que cela conduit à une inversion de la nature des franges.

Bonjour monsieur. Je n'ai pas eu de problème pour la vérification mais je n'arrive pas à comprendre votre explication.

Là c'est maintenant clair.

Merci monsieur pour votre aide.