Niveau autre

looping mécanique

Posté par
Kiecane 02-01-18 à 16:11

Bonjour,

Je suis en train de faire un exercice et je ne comprends pas la correction de celui-ci.
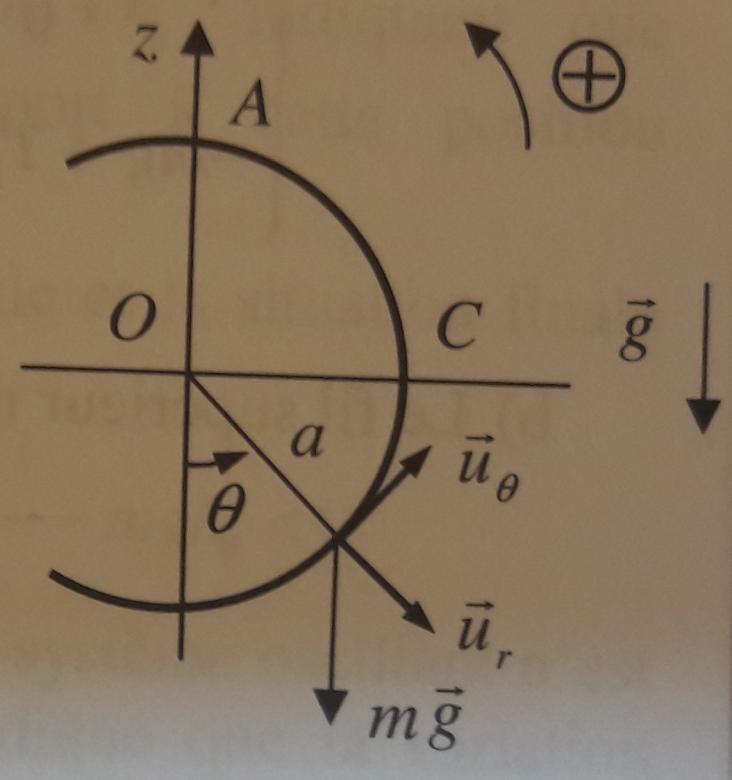
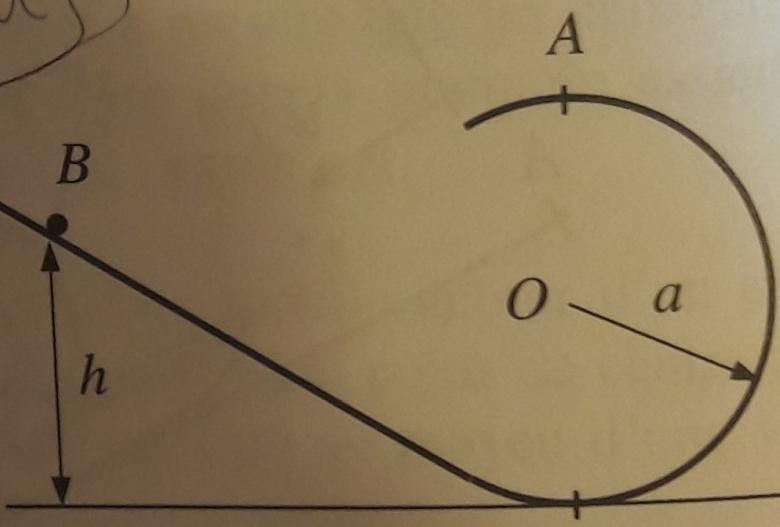
On nous donne le schéma suivant (cf images jointes). On lâche un point matériel de masse m, du point B avec une vitesse initiale nulle. Le mouvement se fait sans frottements et dans le plan vertical. De quelle hauteur doit-on lâcher le point matériel pour qu'il effectue un tour complet du cercle intérieur (c'est-à-dire pour qu'il passe par le point A) ?

Dans la correction il y a écrit : en appliquant le théorème de l'énergie cinétique entre B et M quelconque on a :
1/2 mv²-0=mg(h-(a-acos))+0

Je suppose que c'est égal à mgh-mg(a-acos)+0 avec mgh le travail du poids entre B et le point sur le cercle qui correspond à =0 et -mg(a-acos) le travail du poids à partir de ce point.

J'ai plusieurs questions :

1) Je ne comprends pas comment on peut savoir s'il faut mettre un signe - ou + quand on calcule un travail.

2) Je ne comprends pas comment on trouve a-acos pour le travail du poids entre le point correspondant à =0 et A.

3) Je ne comprends pas à quoi correspond le 0 à droite dans l'égalité. Est-ce que cela correspond à la réaction normale du support et si oui pourquoi est-elle nulle ?

Merci d'avance pour votre aide !

looping mécanique

Posté par re : looping mécanique 02-01-18 à 16:12

looping mécanique

Posté par re : looping mécanique 02-01-18 à 21:28

Bonjour.

Citation :
1) Je ne comprends pas comment on peut savoir s'il faut mettre un signe - ou + quand on calcule un travail.

Par définition, le travail élémentaire d'une force est $dW = \vec{f} . \vec{dl}$
En développant, on a : $dW = f . dl . cos(\vec{f} , \vec{dl})$

si $(\vec{f} , \vec{dl}) < \dfrac{\pi}{2}$      ,     $cos(\vec{f} , \vec{dl}) > 0$      et     $dW > 0$
Un travail positif est dit moteur ; dans ce cas, la force agit dans le même sens que le déplacement.

si $(\vec{f} , \vec{dl}) > \dfrac{\pi}{2}$      ,     $cos(\vec{f} , \vec{dl}) < 0$      et     $dW < 0$
Un travail négatif est dit résistant ; la force agit alors en sens contraire du déplacement.

enfin, pour boucler la boucle, si $(\vec{f} , \vec{dl}) = \dfrac{\pi}{2}$      ,     $cos(\vec{f} , \vec{dl}) = 0$      et     $dW = 0$
On dit alors que la force ne travaille pas.

Concernant le travail du poids d'un corps, oubliez l'expression $W(\vec{P})_{i \rightarrow f} = \pm m g h$      dans laquelle on rajoute le signe $+$ ou $-$ un peu à la sauvette, et retenez plutôt     $W(\vec{P})_{i \rightarrow f} = m g (z_i - z_f)$      $z_i$ et $z_f$ désignant les altitudes initiale et finale du centre d'inertie du solide ; altitudes qui se repèrent sur un axe vertical, orienté positivement vers le haut.

Citation :
2) Je ne comprends pas comment on trouve a-acos

pour le travail du poids entre le point correspondant à

=0 et A.

Les altitudes se repèrent sur l'axe Oz représenté sur le schéma, O étant l'origine de cet axe.

Quand le point matériel est au point le plus bas (où $\theta = 0$ ), on a : $z_i = - a$ (le signe $-$ vient de ce qu'on est sur la partie négative de l'axe Oz)
Lorsque ce même point matériel est dans la position représentée sur le second schéma ( $\theta \neq 0)$ , on a maintenant : $z_f = - a cos \theta$

On aura bien alors : $W(\vec{P})_{i \rightarrow f} = m g (z_i - z_f)$ soit $W(\vec{P})_{i \rightarrow f} = m g [-a - (-a cos \theta)]$ càd enfin $W(\vec{P})_{i \rightarrow f} = -m g (a - a cos \theta) = -m g a (1 - cos \theta)$

Citation :
3) Je ne comprends pas à quoi correspond le 0 à droite dans l'égalité. Est-ce que cela correspond à la réaction normale du support et si oui pourquoi est-elle nulle ?

Je suppose que vous voulez parler du 0 qui est en rouge dans l'expression suivante :
1/2 mv²-0=mg(h-(a-acos

))+0

Ce n'est pas la réaction qui est nulle, mais son travail.
On a, d'après le théorème de l'énergie cinétique, entre B et M : $\Delta E_c = W(\vec{P})_{B \rightarrow M} + W(\vec{R_n})_{B \rightarrow M}$

Or, $dW(\vec{R_n}) = \vec{R_n} . \vec{dl} = 0$ puisque $\vec{R_n} \perp \vec{dl}$ on aura donc bien : $W(\vec{R_n})_{B \rightarrow M} = 0$ .

Est-ce plus clair ?

Posté par re : looping mécanique 03-01-18 à 09:23

J'ai laissé passer ça...

Citation :
2) Je ne comprends pas comment on trouve a-acos

pour le travail du poids entre le point correspondant à

=0 et A.

...si A' est le point où