Inscription / Connexion Nouveau Sujet
Looping : mécanique
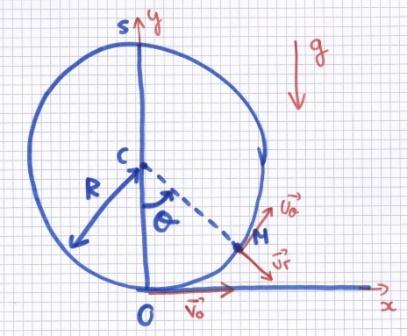
Le but de l'exercice est d'étudier la vitesse initiale pour que le looping soit réussit
il n'y pas de frottement
1. Justifier la direction et le sens de la force de contact F
2. Ecrire les équations du mouvement
je trouve -mR(d
/dt)²=-F+mgcos (en projetant sur ur)
mRd²/d²t =-mgsin
3.A l'aide d'un raisonnement énergétique, déterminer l'expression de F en fonction de ,m,g,v0 et R, En déduire une condition sur pour que la voiture reste en contact avec la piste
(là je suis pas sûr de moi)
on sait que mR(d/ dt)²=m.v0²/R donc F=m(gcos+v0²/R) est-ce juste ?
4.Monter que selon la valeur de v0 trois types de mouvement sont possible : les décrire qualitativement en précisant la condition sur v0 pour laquelle ils sont obtenue .
1/2mv0²+mgz0=1/2mvS²+mgzS
et je trouve v0=(vS²+2g(zS-z0))
et que puis je faire avec ceci pour répondre à la question ?
je vois bien les trois situ
-le looping est réussie
-la voiture quitte la piste car v0 insuffisant
-la voiture reste sur la piste mais repart en arrière car v0 encore plus insuffisant
5.R=15 cm déterminer v0 pour que le looping soit réalisé
Je ne voit pas ce que vaut vS ? (0 m.s-1)?
en prenant vS=0 je trouve v0=2,45m.s-1
6.les autres questions pas encore traitées
Merci de vos lumières !
Edit Coll : image postée sur le serveur de l' 
; merci d'en faire autant la prochaine fois !
Bonjour SOS13,
tu n'as pas repondu a la question 1, mais comme tes reponses a la 2ieme question sont justes je pense que tu avais trouve : la force de reaction F est normale a la trajectoire circulaire en chacun de ses points, donc F est dirigee de M vers C. Ceci parce qu'il n'y a pas de frottement entre M et la piste : une force de frottement serait dirigee en sens contraire de la vitesse, donc tangente a la trajectoire. Il n'y a pas de frottement, donc F n'a pas de composante sur cette tangente. Consequence importante : la reaction F ne travaille pas. Voila ce qu'il faut repondre.
2) OK.
3) je ne vois pas comment tu as obtenu ce resultat : mR(d/dt)2 = mV02/R est surement faux, car le 1er membre varie en fonction de tandis que le 2ieme est constant.
On va appliquer la conservation de l'energie mecanique totale Em = Ec + Ep, ou Ec = 1/2.mv2 est l'energie cinetique de M et Ep l'energie potentielle associee a la seule force qui travaille, cad le poids mg.
a) En prenant l'origine de Ep lors du passsage de M en O, on obtient Em = (1/2)mV02 + rien.
b) lorsque la position de M est definie par l'angle , M s'est eleve de la hauteur OH, ou H et la projection de M sur l'axe vertical Oy. Le travail du poids est Wp = -mg.OH = -dEp, donc l'energie potentielle de pesanteur est Ep = mg.OH (avec le choix de son origine en x = y = 0). On ecrit facilement OH = OC - CH = R(1 - cos).
L'energie cinetique est bien sur Ec = (1/2).mv2 = (1/2).m.R2(d/dt)2.
La conservation de Em donne (1/2).m.R2(d/dt)2 + mgR(1 - cos) = 1/2.m.v02, ce qui fournit une expresseion de la quantite mR(d/dt)2 qui figure dans la 1ere equation du mpuvement obtenue dans la question precedente :
mR(d/dt)2 = mv02/R - 2mg(1 - cos).
On reporte bien sur cette expression dans la relation ou figure F, soit : F = mgcos + mR(d/dt)2 = mv02/R + mg(3cos - 2).
C'est cette derniere relation qui te permet de distinguer les trois types de mouvements, car pour que M puisse atteindre le sommet S de la trajectoire circulaire il faut qu'en S F soit > 0 ou au pire nul. Or S correspond a = 
soit cos = -1 : tu en deduis facilement que pour que ce soit possible il faut que V0 > (5Rg)1/2.
Il y a aussi un autre point critique a placer sur le schema : c'est le point P situe a la meme hauteur que le centre C, cad correspondant a = /2. Il sera atteint si F est positif ou nul en P, soit si V0 = (2Rg)1/2.
D'ou la discussion :
a) V0 < (2Rg)1/2 : M grimpe sur le cercle jusqu'a un angle < /2 (donc l'expression est facile a obtenir), puis redescend en restant en contact avec la piste : le mouvement est oscillatoire.
b) (2Rg)1/2 < V0 < (5Rg)1/2 : l'angle peut depasser /2 mais ne peut pas atteindre la valeur ... le mobile se casse la figure en cours de route.
c) V0 > (5Rg)1/2 : M peut faire un tour complet sur la piste (et comme il n'y a pas de frottement il tournera indefiniment).
Voila... si tu a s des questions n'hesite pas.
Prbebo.
Je me doutais bien qu'il faillait utiliser la conservation de l'énergie mécanique. Un grand merci pour l'explication 
j'aurais peut-être d'autre question.
Pour la question 1 j'ai répondu
la force de contact solide solide est sans frottement, donc la réaction normale du support F à pour direction la droite perpendiculaire à la tangente au cercle au point M et de sens M vers C
cela suffit-il pour répondre à la question ?
Bof non, puisque dire que la reaction normale a pour direction la perpendiculaire a la tangente est une facon de dire deux fois la meme chose. Je prefere de beaucoup mon explication, que je te resume : la force de contact solide-solide est appelee F ; elle possede une composante normale (cad dirigee de M vers le centre de courbure C de la piste), qui existe toujours et assure le contact entre M et la piste, et eventuellement une composante portee par la tangente a la trajectoire ; cette derniere composante, dirigee selon v mais en sens contraire du vecteur vitesse, s'appelle force de frottement. Si on te dit qu'il n'y a pas de frottement, cette composante est nulle et il ne erste que la premiere.
Prbebo.
Annuler
connectez vous