Bonjour,

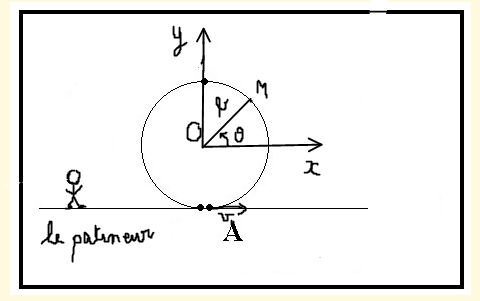
Le patineur est assimilé à un point M de masse m=60.0kg
celui ci se déplace sans frottements à l'intérieur d'un guide circulaire de centre O et de rayon b=2.
Le guide est placé dans un plan vertical du référentiel terrestre supposé galiléen. L'axe (Oy) est la verticale ascendante. On note g=9.8 m.s^-2 l'accélération de pesanteur du lieu considéré.
Le patineur s'élance dans le guide au niveau du point A(en bas du guide) avec la vitesse initiale ₀=v₀.
Dans la suite, on prendra v₀=8.3m.s^-1.
avec (A,,), le repère cartésien et (,) la base polaire : vectreur unitaire radial et orthoradial.

la première partie était sur l'étude du mouvement du patineur dans le guide
je bloque à partir de cette question :

NB : On note M1 le point où le contact cesse, ses coordonnées : x₁=1.73 m ,y₁=1.0 m, vecteur vitesse v₁= 3.2m/s et composantes : v_1x=1.6 m/s et v_1y= 2.8 m/s.
les valeurs numériques sont les résultats que j'ai trouvé dans le début de l'exercice.

6)a- Quelle est la trajectoire suivie ensuite par le mobile après avoir quitté le guide ? On négligera toute forme de frottement dans cette partie.

je pense que c'est une trajectoire parabolique :
bilan des force : P=-mg

j'applique le principe fondamental de la dynamique et j'obtiens a=g (l'accélération)

par intégration : v_x= v_1x
                  v_y= -gt + v_1y

et                x= v_1xt + x₁
                  y= -1/2gt² + v_1yt + y₁

je bidouille un peu l'expression et je trouve comme équation de la trajectoire :
y= -1/2g(x-x₁)²/v_1x² + v_1y(x-x₁)/v_1x + y₁

c'est donc bien une trajectoire parabolique, mais c'est après que ça se complique :

b-Déterminer les composantes v_2x et v_2y de la vitesse lorsque le mobile atteint le sol.
c-En quel point M₂ du sol le point M retombe t-il ?

j'ai essayé de faire quelque chose avec M₂(x,-b)   (dans le repère (Oxy))
j'ai essayé de résoudre y=-b, equation du 2nd degré, je trouve t= 1.1 ou -.56 s
pour t=1.1, ce n'est pas cohérent pour x : je trouve 3.5m, soit en dehors du cercle
et pour t=-.56, je pense que ce n'est pas possible d'avoir un temps négatif.

et pour les composantes de v₂, je ne vois pas du tout comment faire.

merci de votre aide, j'espère avoir été claire.