Bonjour
Pour commencer, as-tu bien compris tous les mots techniques utilisés dans l'énoncé ?
solstice d'hiver, solstice d'été, obliquité, latitude ...
Si oui, il suffit de faire deux schémas clairs correspondant aux deux solutions à étudier. Un minimum de trigonométrie suffit alors...
Peux-tu scanner et poster sur le forum les deux schémas ?

Merci pour votre réponse, voici les schémas:

Le  soleil étant considéré comme extrêmement loin de la terre (distance terre - soleil extrêmement grande par rapport au rayon terrestre), on peut considérer que le soleil éclaire une moitié de la terre. Tu ne semble pas avoir bien compris comment positionner le cercle polaire aux solstices d'hiver et d'été.
Il est midi solaire lors de cette étude, l'obélisque est donc mal placé. Il est dans la zone éclairée et sur le méridien au plus près du soleil.

Pour t'aider un peu, voici un schéma volontairement incomplet et non annoté (à toi de compléter !). C'est un schéma en 2D, le plan de figure contenant le centre de la terre et le méridien sur lequel se trouve l'obélisque (en rouge). Pour plus de clarté, j'ai exagéré la hauteur de celui-ci ; cette hauteur est en pratique très inférieure au rayon terrestre.

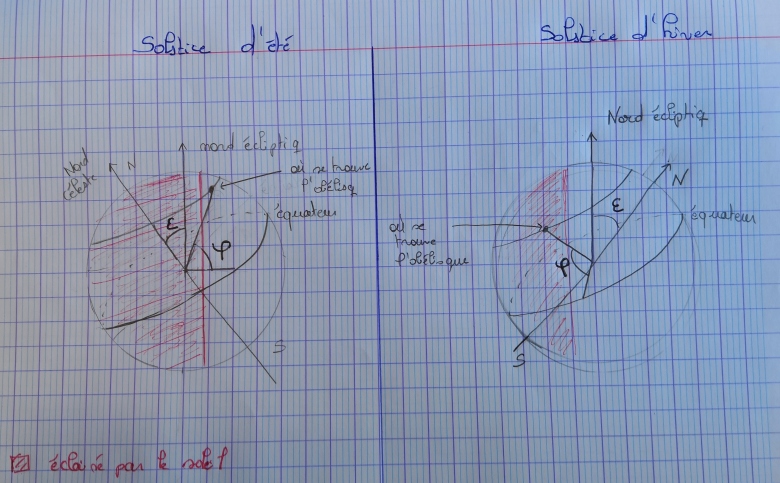
Je pense que le schéma correspond  à un solstice d'été, j'ai placé les angles et ainsi que la longueur h de l'obélisque, mais je ne vois pas comment représenter l'ombre sur le schéma.

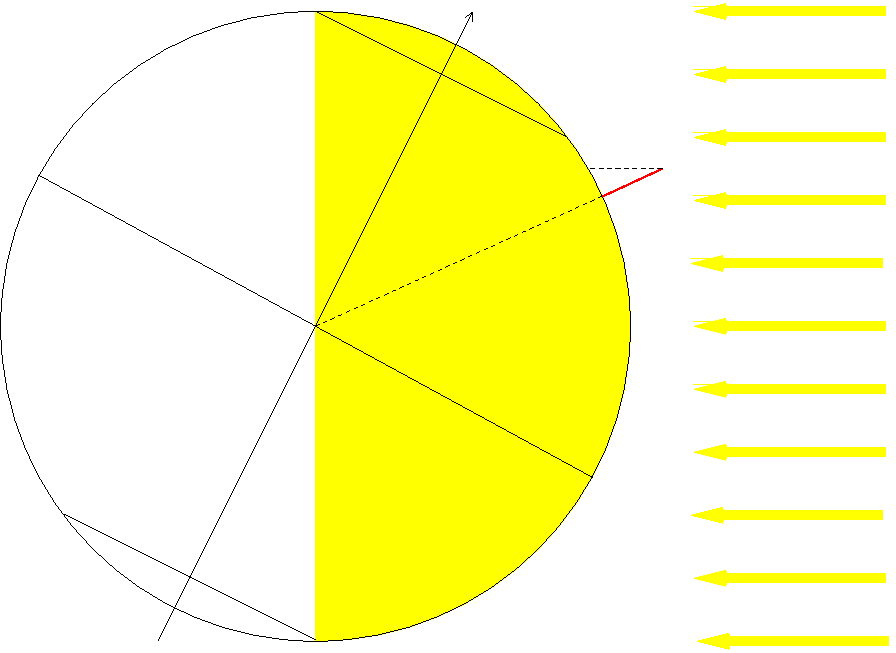
OK pour ce que tu as fait. L'ombre portée est la distance PH. Attention : la figure est un peu trompeuse dans la mesure où h=HS est très petit devant le rayon terrestre. L'arc PH sur la figure est en pratique assimilable à un segment de droite perpendiculaire à HS. La seule difficulté consiste à exprimer l'angle en fonction des données.

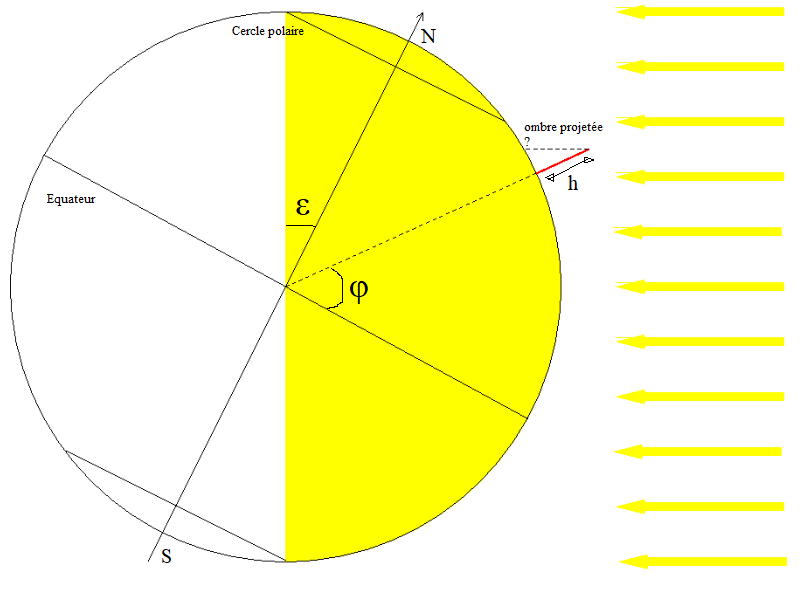
Si on approxime PH  à un segment perpendiculaire à [HS], on a alors la relation suivante :

PH = tan()*HS
Donc il suffit de trouver   en fonction de et pour trouver la longueur PH  de l'ombre.
Mais je n'arrive pas à relier à et , pouvez me donner un indice SVP ? (Les formules trigonométriques suffisent-elles ?)

Si tu prolonges comme je l'ai fait SP de façon à obtenir un triangle rectangle, tu peux écrire simplement :
+ + = /2 rad
Tu as aussi :
+ = /2 rad
Je te laisse terminer et traiter le cas du solstice d'hiver.

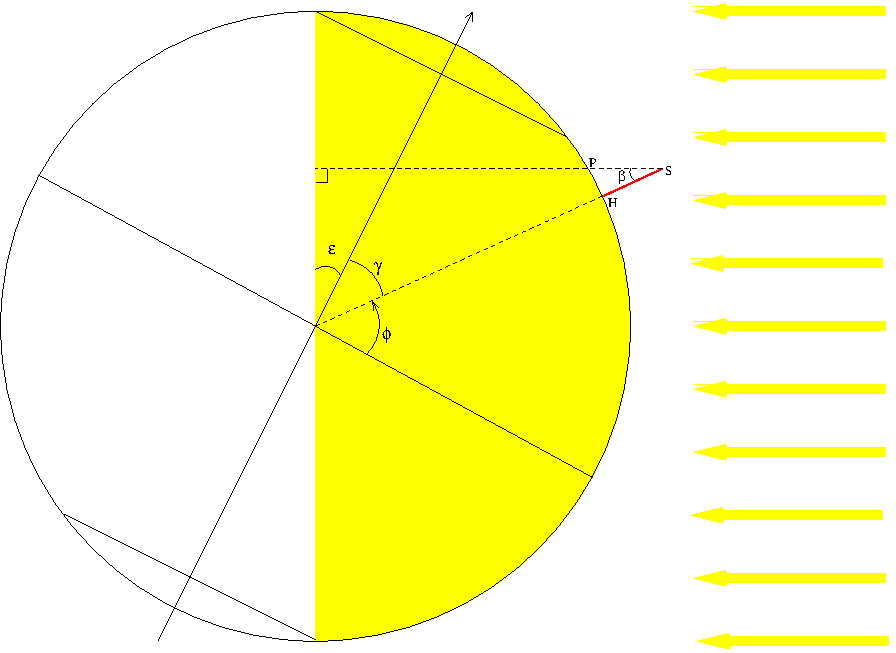
Pour le solstice d'été:
On a ++ = +
Donc = -
On a donc PH=tan( -) *HS

Pour le solstice d'hiver:
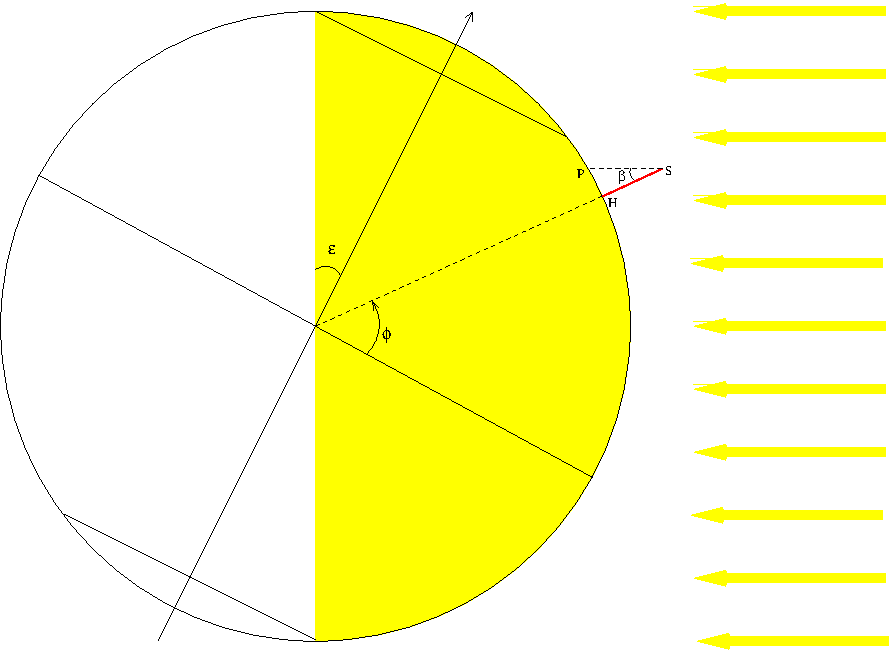
J'ai fait le schéma ci-dessous. J'ai trouvé les relations :
++= ++=/2
Et je trouve =, ce qui n'est pas la bonne réponse, où me suis-je trompée sur le schéma SVP ?

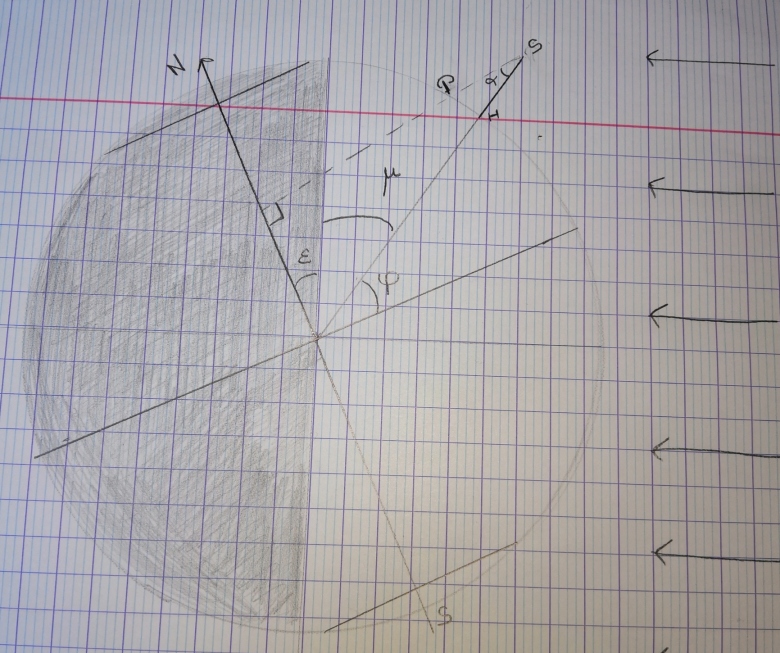
Pour faire simple, on peut remarquer qu'il suffit, par rapport à l'étude précédente, de remplacer par (-).
Sinon, concernant ta figure :
1° : tu as modifié ta convention de coloriage : puisqu'il est midi solaire à l'instant de la mesure, la zone éclairée est l'hémisphère de droite sur ton schéma.
2° : ton point P est mal placé : PS est parallèle aux rayons lumineux émis par le soleil.

D'accord, merci beaucoup pour votre aide !