Inscription / Connexion Nouveau Sujet
Loi d'échelle du vol
Bonsoir , alors voilà je m'entraîne pour des exams et cette exo me pose un peu problème
1. On considère un objet volant selon une trajectoire horizontale, de masse M et de surface alaire S.
Établir la relation entre la vitesse de croisière U et la charge alaire M/S de cet objet. Pour cela,commencer par écrire l'équilibre de l'objet pour obtenir une relation entre la force de portance et le poids. On choisira pour le coefficient de portance la valeur de Cz = 0.6, qui est représentative du vol de croisière.
Comparer les vitesses de croisière d'un Boeing 747 (M = 300 t, S = 500 m2
) et d'un moineau (M = 28 g, S = 7.10−3 m2).
J'ai essayé de commencer à faire quelque chose pour la question 1 voilà où j'en suis mais je ne sais pas si c'est correcte :
Vecteur (Fp)+Vecteur(P)= vecteur nul
Fp=0.5*U²*S*Cz*ro
Fp=-P
0.5*U²*S*Cz*ro=-M*g
U²*S*Cz*ro=-2M*g
U²=-2Mg/SCz*ro
Et pour la deux et la trois je suis bloquée .
2. Règle de similitude : montrer que pour deux objets semblables, c'est-à-dire de tailles différentes mais dont les proportions sont conservées, la charge alaire, M/S, est proportionnelle à M^1/3
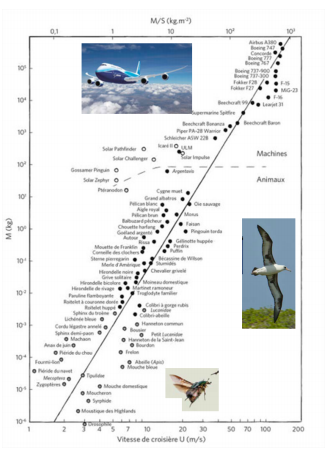
3. Dans le Great Flight Diagram, la relation entre la masse et la vitesse de croisière
dans l'air est décrite approximativement, mais de manière unique, par l'équation U = 16M^1/6 , pour un nombre considérable d'animaux et de machines volantes. Retrouver cette loi d'échelle à l'aide des questions
précédentes. Comment doit-on modifier la masse d'un objet volant si l'on veut multiplier sa vitesse par 2 ?
Merci d'avance pour votre aide .
Bonjour,
Vecteur (Fp)+Vecteur(P)= vecteur nul
Oui
Fp=-P
Non, pas tout à fait, si on projette les forces sur la verticale ascendante,
Fp .... = 0
Fp=.....
2) pour un objet de masse M et de surface alaire S
M ~ a3
S ~ a2
~ signifiant "proportionnel à"
a étant une longueur caractéristique de l'objet
Pour un objet semblable, a devient ka , k étant une constante
Donc M'~ (ka)3
S ' ~ (ka)2
et il faut àpartir de là montrer que M'/S' ~ 3√M'
Bonjour ,merci tout d'abord de m'avoir répondu , je vois pas très bien ce que vous voulez dire par projeter les forces sur la verticale ascendante alors que on est censer être sur une trajectoire horizontale
Pour la 2) M'/S' est donc égale à ka^3/ka^2
en simplifiant par k et par le produit en croix on obtient M'=(a^3*S')/a² en simplifiant par a² on obtient
M'=a^3 est ce que c'est ça ?
bonjour,
je vois pas très bien ce que vous voulez dire par projeter les forces sur la verticale ascendante alors que on est censer être sur une trajectoire horizontale
peu importe la trajectoire, P et FP sont dirigées selon la verticale, et en projection sur cette verticale on trouve:
Fp - P = 0
donc Fp=P et non pas -P
heureusement car sinon on se retrouve avec U2 négatif!!!
Pour la 2) M'/S' est donc égale à ka^3/ka^2
non, M'/S' est proportionnel à (ka)3/(ka)2
les parentheses sont importantes
Ah d'accord pour la projection du coup on obtient U=racine de (2Mg/SCz*ro)
Pour la question 2 du coup si je reprends ça fait M'S' proportionnel à (ka)^3/(ka)²
ainsi M'S' proportionnel à ka
et M'=ka/a² et donc M'=k/a
M'S' proportionnel à ka
petite erreur de frappe
C'est M'/S' ~ ka
Mais M'~ (ka)3 donc ka ~ 3
 M'
M'
D'où le resultat
Ensuite y faut que j'utilise la formule trouver à la question 1 c'est bien ça ? Mais je la simplifie de façon à n'avoir que U=M/S ?
Je ne comprends pas ce que tu fais
On a une relation du type
U²=kM/S avec k= cste = ....
et M/S ~ 3  M
M
donc U ~ ...
Oui pardon , mais je n'arrive pas à retomber sur la valeur 16 c'est en calculant k que je l'obtient c'est ça ?
parce que j'ai pris g=9.81 , Cz=0.6 d'après énoncé et ro de l'air = 1.3 kg/m^3
d'accord merci et du coup juste pour la dernière partie de la question
Comment doit-on modifier la masse d'un objet volant si l'on veut multiplier sa vitesse par 2 ?
On doit diviser la masse par 2 si on veut multiplier sa vitesse par 2
U =16 M 1/6
2U = 16 M' 1/6
Donc 2U/U = 2 = 16 M '1/6 / (16 M1/6)
Donc (M '/M)1/6 = 2
Donc M'/M = ....

 ,
,  16 M 1/6
16 M 1/6

