Inscription / Connexion Nouveau Sujet
Lithographie électronique
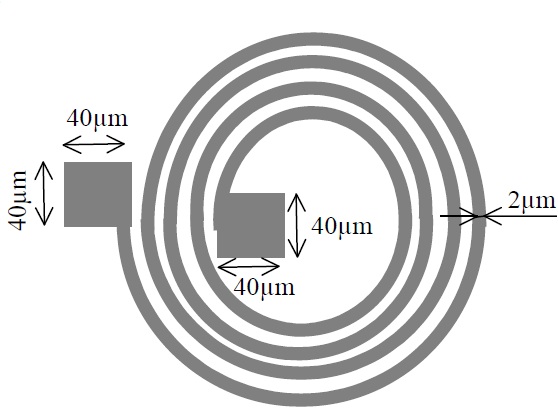
On désire réaliser par lithographie électronique et lift-off une microbobine, constituée de n = 20 spires, de rayon allant de rmax = 150um à rmin = 100 μm (voir figure ci-dessous, sur celle-ci, seules 4 spires ont été représentées). On dispose d'une résine ayant une sensibilité de 400 μA.s.cm-2.
1) Quelle unité du système SI aurait-il été logique d'utiliser? Que vaut la sensibilité de la résine avec cette unité?
2) La largeur des spires est de 2 μm. Calculer la surface que représente la surface conductrice de cette spire (on pourra assimiler chaque spire à un cercle). On ajoute 2 plots carrés de 40x40μm2 pour pouvoir réaliser les contacts électriques. Quelle est la surface totale S à insoler?
3) Le faisceau d'électrons a une intensité de I = 20 pA = 20x10-12 A. En négligeant les durées de transfert du faisceau d'électrons, combien de temps doit durer l'insolation?
Réponses:
1/ Unite SI : C.cm-2 car [A]= [C].[s[-1
dans ce cas, La sensibilité est de 4*10-4 C.cm-1
2/ Pour calculer la surface de la spire conductrice, faut il calculer la surface du cercle de rayon r puis celui de rayon r-l (l : largeur de la spire) puis soustraire, quel rayon utiliser ? ( on multiplie par 20 pour trouver la surface total conductrice en ajoutant la surface des deux carres)
2/ Multiplier la sensibilité de la résine par la surface puis diviser par l'intensité.
Pouvez vous m'aider pour la seconde et voir s'il y a incohérences pour les autres s'il vous plait?
Merci
Bonjour,
1) Cela me semble plausible d'un point de vue unité SI mais je ne sais pas ce qu'est la sensibilité de la résine à un courant! Mais je vois sur Wikipédia que l'insolation est un rayonnement UV visant à changer les propriétés de la résine et on parle de J.m-2
2) Soit lC la largeur des spires de cuivre et lR la largeur des spires de résine
On a donc 20 * lC + 19 * lR = Rmax - Rmin
D'où lR = ((150 - 100) - (20 * 2)) / 19 = 10/19 
m
Le rayon de la première spire sera r1 = Rmax - lC/2
Le rayon de la spire suivante sera alors r2 = r1 - (lC+lR)
Appelons lD = (lC+lR) donc r2 = r1 - lD
Le rayon de la n+1 ème spire sera : rn+1 = rn - lD
On a donc affaire avec une suite arithmétique de premier terme r1 et de raison -lD
Donc on a rn = r1 - (n-1)lD
La surface de la spire de cuivre n est donc donnée par Sn = 2
rn * lC
La surface des 20 spires de cuivre est donc égale à SC = 
n=1 à 20 (2rn * lC)
D'où SSC = 2 * lC * n=1 à 20 (rn)
Soit SSC = 2 * lC * ((20 * r1) - n=1 à 20 ((n-1)*lD))
Soit encore SSC = 2 * lC * ((20 * r1) - (lD * n=1 à 20 (n-1)))
Càd SSC = 2 * lC * ((20 * r1) - (lD * (19*20/2)))
En définitive SSC = 2 * lC * ((20 * r1) - (190 *lD))
Je ne connais pas l'opération d'insolation: je ne sais pas quelle est la surface à insoler, celle de cuivre ou celle de non-cuivre? D'ailleurs je parle de cuivre mais Est-ce réellement le matériau conducteur de la bobine à constituer?
3) Même remarque que précédemment
A toi donc de finaliser en vérifiant ce que j'ai fait
Bonjour,
Merci pour votre réponse.
Mais pourquoi introduire la largeur des spires de résine ? Il y a des spires de résine ?Je n'ai pas bien compris
Ce que j'ai appelé spires de résine correspond aux intervalles circulaires entre ce que j'ai appelé les spires de cuivre
Mais comme je l'ai expliqué, je ne connais rien à la fabrication de circuits imprimés (malgré ma formation initiale et toute ma carrière passée dans les équipements Télécoms: un constat assez désarmant au passage!)
Annuler
connectez vous