Inscription / Connexion Nouveau Sujet
les ondes
svp est ce que vous pouvez m aider dans cette question :
Exprimer mathématiquement une fonction non harmonique pouvant représenter une onde qui se propage.
Bonjour
Tu as déjà posé cette question il y a trois jours.
Relis bien ton cours, tu y verras qu'un signal s correspondant à une onde se propageant dans le sens des x positifs correspond à une fonction quelconque de la variable :
Dans ce contexte, une fonction harmonique est simplement une fonction sinusoïdale. Il te faut donc exclure ici les expressions de la forme :
où A, ,
, sont des constantes.
sont des constantes.
Je te laisse continuer l'exercice... 
Merci pour votre réponse , oui je sais qu'est ce que une fonction harmonique mais le problème c est que je sais pas qu'est ce que c'est une fonction "non harmonique" pouvant représenter une onde qui se propage . c 'est cela ce que j'ai pas compris , pourriez vous me donner un exemple de cette fonction svp ?
Puisque tu as expliqué dans l'autre post qu'il s'agit d'une question "ouverte", j'imagine que le concepteur de l'énoncé considère comme acceptable toute fonction autre que sinusoïdale.
Tout à fait au hasard : une exponentielle décroissante :
où a est une constante positive ayant la dimension de l'inverse d'un temps et A une constante quelconque ayant la dimension de s ...
Sous réserve d'avoir bien interprété l'énoncé...
Je vous remercie beaucoup monsieur , oui c'est tout a fait une fonction quelconque , mais comment on peut déterminer la vitesse d'onde à partir de cette équation ?
est ce que c'est bien la célérité "c" sachant que cette onde se propage à une dimension dans un repère (O , x)
Tu peux vérifier que cette célérité est c en montrant que s vérifie l'équation différentielle de propagation de d'Alembert et en identifiant...
j ai trouver que c=racine de t0/µ . est ce que c est bien cela ? sachant que j ai suppose que cette équation est bien de d'alembert parceque je sais pas comment on peux vérifier que c'est une équation de d'alembert
Bonjour
J'ai l'impression que tu essaies de te “raccrocher” à une formule donnant la célérité d'une onde transversale le long d'une corde élastique. Cela n'a rien à voir avec ce problème ! Comment écris-tu l'équation différentielle de propagation de d'Alembert ? Il suffit de l'appliquer à l'expression de s(t,x)...
on sait que l'équation de d'alembert s'ecrit sous la forme : javascript:void(0)
donc j'ai fait la dérivée seconde de s(x,t) par rapport à x aprés par rapport à t , alors de la je fais comment pour extraire l'expression de c ( la célérité ) .
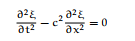
on sait que l'équation de d'alembert s'ecrit sous la forme :
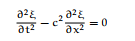
donc j'ai fait la dérivée seconde de s(x,t) par rapport à x aprés par rapport à t , alors de la je fais comment pour extraire l'expression de c ( la célérité ) .
Par contre cette question :
"Quelle est l'expression de cette onde si la vitesse de propagation varie linéairement avec la variable d'espace x ?"
je l'ai pas compris ca veut dire quoi "la vitesse de propagation varie linéairement avec la variable d'espace x" ?
Tu peux remplacer dans l'expression de s(t,x) "c" par une fonction affine de x : a.x+b par exemple ou a et b sont deux constantes. Tu vas alors pouvoir montrer que cette nouvelle expression ne vérifie pas l'équation de propagation de d'Alembert et ne correspond donc pas à une onde se propageant sans amortissement dans un milieu homogène. Logique : dans un milieu homogène, la célérité est une constante, pas une grandeur dépendant de x !
Merci beaucoup , juste pour verifier que cette nouvelle onde ne vérifie pas l'équation de d'alembert est ce que je dois faire la même chose c est a dire je fais encore les dérivées secondes par rapport à x et à t , après je dois remarquer que la célérité est une grandeur dépendant de x ? est ce que c'est bien comme cela ?
Merci beaucoup monsieur , en fait si vous m'excuser j 'ai eu des problemes au niveau d'un autre exercice sur "Traitement antireflet" qui dit :
On considère une lumière monochromatique.
1) Au passage d'un milieu d'indice n1 à un milieu d'indice n2, le coefficient de réflexion de
l'amplitude lumineuse, en incidence normale, est : 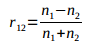
Évaluer la perte d'énergie lumineuse pour un objectif comprenant 4 lentilles d'indice n = 1,5
placées dans l'air. On utilisera un développement limité à l'ordre 1 pour l'application numérique.
est ce que vous pouvez m'aider dans cette question svp ?
Il te faut créer un nouveau topic et fournir l'énoncé intégral de l'exercice. Sinon, difficile de t'aider...


