Inscription / Connexion Nouveau Sujet
les filtres
Salut, je suis entrain de faire l'étude d'un filtre (second ordre, passe bas). Ce qui me pose problème c'est l'expression finale de la fonction de transfère (note :
,
)
Peut être que la calcul est bon, mais est ce que c'est la bonne expression finale ? (PS : dans l'énoncé on ne me donne pas l'expression de que je devrais trouver) merci.
*** image placée sur l'
***
oui, en fait je sais que je ne me trompe pas au niveau des calculs mais je me dis que l'expression finale de H(jw) ne ressemble pas aux expression générale de H(jw) des différents type de filtres.
Peut être qu'il faut exprimer H(jw) autrement.
Impédance de C: Z1 = 1/jwC
Impédance du RLC: Z2 = R + jwL - j/wC = R + j(wL - 1/wC) = R + j(w²LC - 1)/wC
Z2 = (wRC + j(w²LC - 1))/wC
Us/Ue = Z1/Z2
Us/Ue = wC/[jwC * (wRC + j(w²LC - 1))]
Us/Ue = 1/[(jwRC - (w²LC - 1))]
Us/Ue = 1/[(1 - w²LC) + jwRC]
Et en posant LC = 1/wo² et Q = L.wo/R
wRC = wRLC/L = wR/(wo².L) = wR/(wo.Q.R) = w/(Q.wo)
--> Us/Ue = 1/[(1 - (w²/wo²)) + jw/(Q.wo)]
J'ai donc la même réponse que la tienne.
-----
Sauf distraction. 
Salut Skops.
L'expression sous la forme donnée par Skops est très souvent utilisée et se prète bien à établir les diagrammes de Bode.
justement pour établir le diagramme de Bode moi j'ai utilisé directement l'expression de H(jw) :
D'où :
Puis, pour calculer les asymptotes on se met en basses fréquence où w tend vers +
et en hautes fréquences où w tend vers
Le problème, c'est que quand w tend vers + en basse fréquences, l'expression de Gdb reste la même, il y a rien qui se simplifié. Comment trouver l'équation de l'asymptote dans ce cas là avec ?
Re
En +oo, tn (w²/w0²)² est prépondérant devant tous les autres termes donc tu as Gdb=-10log(w^4/w0^4)
Skops 
et donc Gdb = -40 log w/w0
Normalement ici on a un filtre passa bas. Si on trace la courbe du diagramme avec Gdb = -40 log w/w0 on vois que la courbe tend vers 0 en - infini. ça ne devrait pas être le cas puisque c'est un passe bas non ?
Justement, puisque c'est un passe bas, il va laisser passer les basses fréquences donc le gain ne changera pas
Par contre, en +oo, tu auras une forte atténuation des fréquences ce qui se traduit par une limite en +oo de _oo avec une pente de _40dB/dec
Skops
ah non, j'ai fais une fausse interprétation de la courbe. Le résultat est bon.
Je doit calculer la valeur de w pour laquelle Gdb est maximum. On pourra dériver l'expression de Gdb mais combien vaut la dérivée de log ? je ne pense pas que c'est comme ln(x) en tout cas.
y a il une autre méthode pour trouver le maximum de gdb ?
Je viens de remarquer que ton module est faux, tu n'as pas pris la partie réelle quand tu as mis au carré sous la fraction 
On a un max de Gdb quand on a un min de ce qu'il y a à l'intérieur
Skops
A partir de H(w) = 1/(1 - jw/(Q.wo) + (jw)²/wo²)
On a directement les asymptotes du Diagramme de Bode.
Pour le gain :
asymptote horizontale sur 0 dB (pour les basse fréquence)
Coupure pour w = wo à descente à 40 dB par décade, donc à partir du point 0dB et pour w = wo, asymptote oblique descendant à 40 dB par décade.
-----
On peut évidemment aussi le retrouver à partir de Us/Ue = 1/[(1 - (w²/wo²)) + jw/(Q.wo)]
G = - 20 log[V((1 - (w²/wo²))² + w²/(Q.wo)²)]
si w -> 0, G tend vers -20 log(1) = 0 dB (première asymptote, horizontale sur 0 dB)
Si w -> +oo, le terme en w^4 écrase les autres et G -> 20 log(V(w²/wo²)^2) = -40 log(w/wo)
Et donc la seconde asymptote passe par O dB en w = Wo et descend à 40 dB par décade.
----
Pour le tension de sortie max: en posant w/wo = X
f(X) = (1 - X²)² + X²/Q²
f '(x) = -4X.(1-X²) + 2X/Q²
f '(X) = 0 pour 4X.(1-X²) = 2X/Q²
2.(1-X²) = 1/Q²
1-X² = 1/(2Q²)
X² = 1 - (1/2Q²) = (2Q² - 1)/2Q²
w²/wo² = (2Q² - 1)/2Q²
w² = wo² * (2Q² - 1)/2Q²
Et donc si Q est très grand, Us est maximum pour
On remarque aussi qu'il n'y a pas de surtension si Q < 1/V2
Si Q > 1/V2, la tension de sortie est max pour w = wo * racinecarrée[(2Q² - 1)/2Q²]
Exemple numérique:
Si Q = 2, Us est max pour w = Wo * V(7/8) = 0,935.Wo
Et à cette pulsation :
G = - 20 log[V((1 - (0,935²))² + 0,935²/2)] = + 3,44 dB
-----
Sauf distraction.
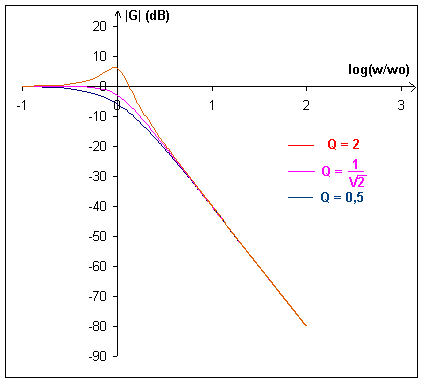
Je me demande comment elle est la courbe de Gdb pour les valeurs de :
=
A moins que l'allure de la courbe ne dépend pas du facteur de qualité (ce qui m'étonnerais).
j'ai tracé ces courbes mais je n'en suis absolument pas sûr.
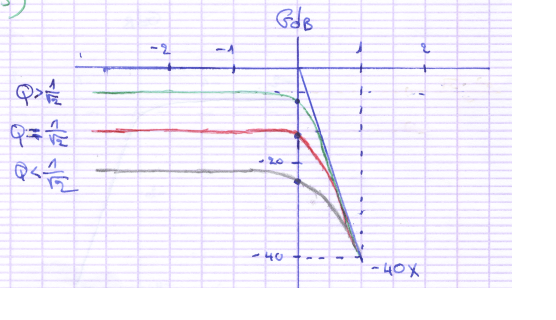
Je pense que il faut peut être mettre des pic pour chacune de ces coures en
ah non, je pense avoir trouvé la faute.
On a le maximum lorsque
Ce maximum existe si
Donc a une allure normale sans pic mais les deux autre devrait en avoir.
D'après les calcul w existe pour w inférieur à 1/racine(2) non ? pourquoi ce n'est pas le cas sur la courbe ?
je me suis trompé, je voulais dire que normalement d'après le calcul w existe pour w différent de 1/racine(2) non ? donc pour Q inférieur à 1/racine(2) il doit y avoir un pic.
pourquoi ce n'est pas le cas sur la courbe ?
J'ai montré que :
f(X) = (1 - X²)² + X²/Q²
f '(x) = -4X.(1-X²) + 2X/Q² (et X >= 0)
f '(X) = (2X/Q²).(2Q².(X²-1) + 1)
Détermination du signe de (2Q².(X²-1) + 1)
Racines de (2Q².(X²-1) + 1) = 0
2Q²X² = 2Q² - 1
X² = (2Q² - 1)/(2Q²)
Si le membre de droite est < 0, il n'y a pas de solution (puisque, à cause du carré le membre de gauche est >= 0)
--> Pas de racine si 2Q²-1 < 0, soit si Q < 1/V2
Donc si Q < 1/V2, (2Q².(X²-1) + 1) est du signe de son coefficient en X², soit positif.
Donc si Q < 1/V2, f '(X) > 0 et donc f(X) est croissante.
f(0) = 1 et donc f(x) > 0 pour tout x >= 0
Comme f(x) est croissante et positive , V(f(x) existe, est strictement positive) et est croissante.
ln(V(f(X)) existe et est croissante.
- ln(V(f(X)) existe et est décroissante.
Donc si Q < 1/V2, - ln(V((1 - X²)² + X²/Q²) est décroissante.
Et comme X = w/wo :
si Q < 1/V2, G = - 20.ln(V((1 - (w/wo)²)² + (w/wo)²/Q²) est décroissant.
Il n'y a donc pas de maximum local à G(w) si Q < 1/V2
-----
Sauf distraction.
Annuler
connectez vous