Inscription / Connexion Nouveau Sujet
Lentille demi-boule, stigmtisme et approximation de gauss
Bonjour,
je suis en prépa et j'ai un exercice d'optique à faire, sauf que j'ai beau chercher partout je ne vois pas du tout avec quelles lois ou quelle "stratégie" je peux résoudre cet exercice.
Voici l'exercice: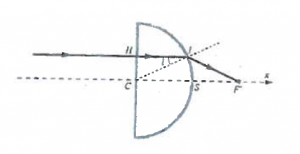
Merci d'avance!
***Image recadrée --> un énoncé est à RECOPIER***
Hello
Quelle loi: 2nde loi de Descartes
Quelle stratégie: se rappeler les cours de géométrie du collège
Au moins pour démarrer 
Soit I' le projeté de I sur l'axe x:
Snell-Descartes: n.sin(i) = sin(i') (i' étant l'angle entre le le (CI) et le rayon réfracté (IF') )
Géométrie:
IF' = II' / sin(i'-i)
II' = R.sin(i)
Sauf grosse bourde de ma part (ça arrive)
presque i' est l'angle du rayon réfracté tel que représenté dans le loi de Snell Descartes
c'est (pi - i') dans la représentation du i' que tu donnes sur ton schéma.
D'après la loi de snell descartes, l'angle i' est celui-ci, la droite rouge étant la tangente à la surface au point I
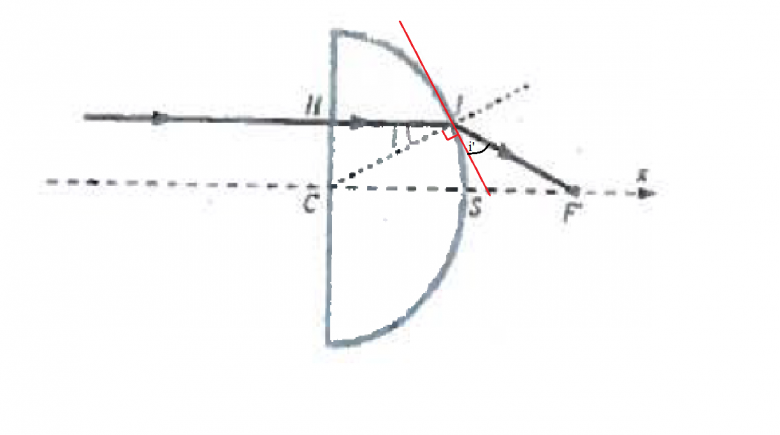
D'après la loi de snell descartes, l'angle i' est celui-ci,
NON c'est pi/2 moins l'angle que tu dessines!
Ah oui d'accord je visualise !!!
Donc le chemin optique = HI + IF'
= R.cos(i) + IF'
= R.cos(i) + II' / sin(i'-i)
=R.cos(i) + R.sin(i)/sin(i'-i)
et pour aller plus loin sin(i'-i) = sin(i')cos(i) - cos(i')sin(i)
Est-ce bien ça?