Inscription / Connexion Nouveau Sujet
Légolas et le gouffre de Helm
Bonsoir, j'aimerais un peu d'aide pour cet exercice. Merci
ENONCE
Durant la bataille du gouffre de Helm et malgré tous les efforts fournis pour repousser l'armée d'Huruk-Hai, une breche est ouverte et les orcs pénètrent dans la forteresse de For-le-Cor.
Légolas, auparavant posté sur la muraille, décide de descendre dans la cour pour poursuivre la bataille. Le moyen le plus rapide qu'il choisit pour descendre implique une glissade dans les escaliers sur un bouclier.
On étudiera le mouvement de Légolas et du bouclier, assimilés à un point matériel L, sur les escaliers représentés par un axe (Ox) faisant une angle 
avec l'horizontale.
-L'air exerce une force de frottement supposé de la forme où
> 0 et
est la vitesse de Légolas.
- On note et
les composantes Tangentielles et normale de la force de frottement exercée par les marches sur le bouclier.
est le coefficient de frottement solide tel que puisque le bouclier glisse.
On choisit comme origine de l'axe (Ox) la position initiale de Légolas, en haut des escaliers. On note (Oy) la normale à l'escalier dirigée vers le haut.
1. A l'aide du PFD, calculer
2. Calculer la vitesse puis la position x de Légolas à chaque instant.
3. Montrer que Légolas atteint une vitesse limite et ré-exprimer
en fonction de
.
4. A.N: = 1,
= 0,9, g = 9,81 , m= 80kg ( principalement le poids du bouclier, Légolas etant un elfe) et
= 45°
5. Calculer littéralement et numériquement la date où Légolas atteint une vitesse égale à
.
6. A la date t_1, Légolas atteint un point sur l'escalier recouvert par des cadavres d'orcs, vaincu par Gimli. On considère que le coefficient de frottement sur le sol est multiplié par 10 et on néglige alors la résistance de l'air.
Calculer la distance parcourue par Légolas avant de s'arreter.
Bonsoir
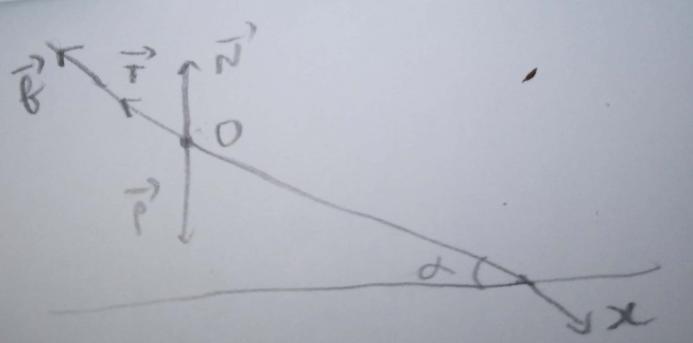
Commence par faire un schéma soigné où seront représentés les vecteurs forces. Propose ensuite un début de solution en expliquant avec précision ce qui te bloque.
Comme son nom l'indique, la réaction normale N est perpendiculaire au plan incliné.
Ensuite : projection de la relation fondamentale de la dynamique sur deux axes : un parallèle et l'autre perpendiculaire au plan incliné.
il ya quelque chose qui me bloque.
L'exercice parle de composante normale de la force de frottement. Dois je la representer ? et comment
De plus quelle est la différence entre cette composante et la reaction N ?
On peut considérer la force exercée par le plan incliné sur le solide qui glisse possède deux composantes, une composante normale et une composante tangentielle
. Écrire cela revient à considérer l'action du plan incliné sur le solide comme une somme de deux forces : la réaction normale et la réaction tangentielle.
On peut donc au choix parler de composante normale ou de réaction normale : c'est la force perpendiculaire au plan incliné. Corrige donc ton schéma en tenant compte de cela.
d'apres le PFD
sur l'axe (Ox)
on a : mgsin -T + 0 -v = 0 
T = mgsin - v
sur l'axe (Oy)
on a : -mg +0 + N + 0 = 0 N = mg
Plusieurs remarques :
1° : La projection du poids sur l'axe des y n'est pas égale à P. Ton expression de N est donc fausse.
2° : L'accélération n'est pas nulle dans le cas général. Il te faut revoir la projection du PFD sur l'axe des x.
3° : T s'obtient simplement à partir de N par la relation fournie dans l'énoncé :
oui je me suis trompé excusez moi .
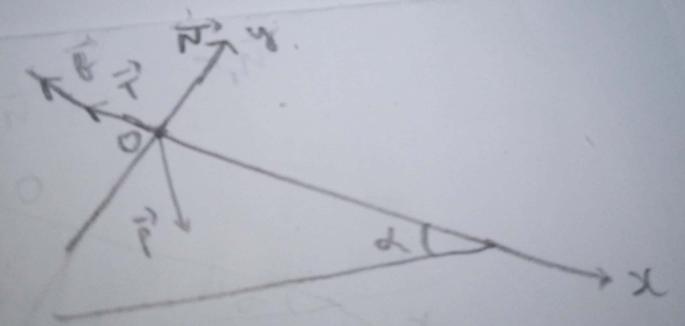
Mais je voulais savoir mon schéma est-il correct ? y a t'il des données en trop ou en moins ?
d'apres le PFD
sur l'axe (Oy) on a :
-mgcos + 0 + N + 0 = 0 N = mgcos
De plus donc T =
.mgcos
D'accord avec tes expressions de N et T. Il te faut maintenant projeter le PFD sur l'axe (Ox) puis répondre aux autres questions.
Compte tenu de la projection du PFD sur l'axe (Ox) que tu as obtenue, de la définition de l'accélération et de l'expression de la force f fournie par l'énoncé, la vitesse est solution d'une équation différentielle du premier ordre que l'on sait résoudre au niveau bac+1 :
Essaie de retrouver cette équation ; attention à la projection du poids sur l'axe (Ox).
Ensuite, il faut résoudre cette équation différentielle.
L'axe (Ox) étant orienté dans le sens du mouvement, la vitesse est toujours positive. Je pense qu'il y a un problème de signe dans ton expression de v(t).
Pour obtenir x(t), il faut effectivement déterminer une primitive de v(t) puis déterminer la constante d'intégration en posant x=0 si t=0.
Tu as dû étudier en math la primitive par rapport à t de exp(-a.t) où a est une constante réelle.
Annuler
connectez vous