Inscription / Connexion Nouveau Sujet
le temps de vidange
bonsoir tout le monde, j'aurais bien besoin svp de votre aide afin de me corriger . je vous remercie par avance
voici l'énoncé:
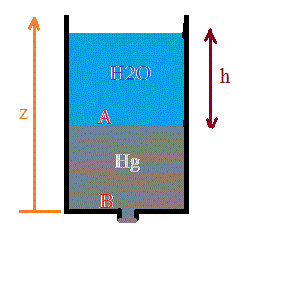
Un Vase cylindrique, de hauteur 2h et de section S, ouvert à sa partie supérieure est rempli :
De mercure dans la moitié inférieure,
d'eau dans la moitié supérieure.
On perce dans le fond un orifice à mince paroi, de section ɯ négligeable par rapport à celle du vase, dont le coefficient de contraction, supposé constant est m. Si K est le rapport des masses volumiques de l'eau et du mercure, quel sera, évalué en fonction de h, s, m et K, le temps nécessaire pour que la vase se vide complément ?
Solution :
Deux façons pour écrire le volume vidangé pendant un temps dt d'une part en fonction du débit Qv et d'autre part en fonction de la baisse de niveau dh dans le réservoir pendant ce temps dt .
Le débit volumique s'écoulant à travers l'orifice est : Qv .ɯ. √(2.g.h(t)) (où ɯ est la section de l'orifice).
Le volume vidangé pendant un temps dt est Qv.dt = -S.dh(où S est la section du vase ou le volume à vider) : on égale le volume d'eau Qv.dt qui s'écoule par l'orifice pendant le temps dt et le volume d'eau -S.dh correspondant à la baisse de niveau dh dans le réservoir. Le signe moins est nécessaire car dh est négatif (puisque le niveau dans le vase baisse) alors que l'autre terme (Qv.dt) est positif.
m étant coefficient de contraction de l'orifice
Ainsi :
m .ɯ. √(2.g.h(t)). dt = -S.dh, dont on peut séparer les variables ( m .ɯ.√(2.g))/(-S) .dt = dh/( √h)= h -1/2 .dh
On peut alors intégrer ( m .ɯ.√(2.g))/(-S).∫_0^t▒〖dt=〗 ∫_0^h▒h -1/2 .dh , soit ( k .ɯ.√(2.g))/(-S).t
D'où
t = ( 2.S)/(m.ɯ) x √(h/(2.g) )
Il faut séparer le problème en 2 phases.
1) Une phase avec le Hg et l'eau présents dans le réservoir.
2) Une phase où il ne reste plus que de l'eau dans le réservoir (le Hg ayant déjà été vidé entièrement).
Calcul de la vitesse d'écoulement du fluide par le trou dans la phase 1 :
Bernoulli :
PA + RhoHg .g.ZA + RhoHg.VA²/2 = PB + RhoHg .g.ZB + RhoHg.VB²/2
Avec PA = Po + Rhoeau.g.h
et PB = Po (pression atmosphérique)
et on a : VA 0 (puisque s < < S)
On a alors, en posant ZA-ZB = z (hauteur de Hg restant dans le réservoir) :
On peut en déduire le débit en fonction de z et puis la variation de hauteur de Hg restant dans le réservoir ... et en déduire la durée pour que le Hg soit complètement sorti du réservoir.
*****
On se retrouve alors dans la phase 2 qui débute avec une hauteur h d'eau (seule) qui s'évacue par le trou ...
En appelant z cette fois la hauteur d'eau restant, la vitesse de vidange est alors
... et on peut calculer la durée de vidange de l'eau.
Au final, en ajoutant les 2 durées calculées, on a la durée totale de la vidange.
Sauf distraction. 
J-P pour la vitesse d'écoulement du fluide par le trou c'est:
PA + RhoH2O.g.ZA + RhoH2O.VA²/2 = PB + RhoHg .g.ZB + RhoHg.VB²/2
au lieu de:
PA + RhoHg .g.ZA + RhoHg.VA²/2 = PB + RhoHg .g.ZB + RhoHg.VB²/2 ?????
Ben non.
Dans la 1ere phase, c'est du Hg qui coule par le trou et c'est du Hg qu'il y a partout entre les niveaux A et B.
... et donc la relation est bien : PA + RhoHg .g.ZA + RhoHg.VA²/2 = PB + RhoHg .g.ZB + RhoHg.VB²/2
Mais évidemment, la pression PA dépend bien de la hauteur d'eau au dessus du Hg et on a : PA = Po + Rhoeau.g.h
-----
Mais évidemment, lorsque la totalité du Hg aura coulé, il ne restera plus que de l'eau ...
et la vitesse d'écoulement sera différente de celle calculée en phase 1, comme je l'ai écrit dans mon message précédent.
Sauf distraction.
....et le volume vidangé pendant un temps dt en fonction de la baisse de niveau dh dans le réservoir ( pendant ce temps dt ) sera:
dt= (S/m.s)(dh/VB )
la durée pour que le Hg soit complètement sorti du réservoir:
t= (2.S.Z) / m.s. 
2g (
eau. h +Hg.z)/ Hg.
J-P peux tu me dire est ce que j'ai bien compris ?
Il ne peut pas y avoir de z dans la réponse finale du temps de vidange.
Qvol = s.vB
dV/dt = -s.VB
avec V = S*z et donc dV = S.dz
S.dz/dt = -s . VB
S.dz/dt = -s . RCarrée(2g.(Rhoeau.h + RhoHg.z)/RhoHG)
dz/RCarrée(2g.(Rhoeau.h + RhoHg.z)/RhoHG) = -s/S dt
dz/RCarrée((Rhoeau.h + RhoHg.z)) = -s/S * RCarrée(2g/RhoHG) dt
On intègre :
(2/RhoHG).RCarrée((Rhoeau.h + RhoHg.z)) = -s/S * RCarrée(2g/RhoHG) * t + K
en t = 0 , z = k -->
(2/RhoHG).RCarrée((Rhoeau.h + RhoHg.h)) = K et donc :
(2/RhoHG).RCarrée((Rhoeau.h + RhoHg.z)) = -s/S * RCarrée(2g/RhoHG) * t + (2/RhoHG).RCarrée(h(Rhoeau +RhoHg.h)
s/S * RCarrée(2g/RhoHG) * t = (2/RhoHG).RCarrée(h(Rhoeau +RhoHg)) - (2/RhoHG).RCarrée((Rhoeau.h + RhoHg.z))
s/S * t = Rcarrée(2/(g.RhoHG)).RCarrée(h(Rhoeau +RhoHg)) - Rcarrée(2/(g.RhoHG)).RCarrée((Rhoeau.h + RhoHg.z))
t = S/s * Rcarrée(2/(g.RhoHG)) * [RCarrée(h(Rhoeau +RhoHg)) - RCarrée((Rhoeau.h + RhoHg.z))]
En appelant T1 la durée de vidange du Hg, il vient :
T1 = S/s * Rcarrée(2/(g.RhoHG)) * [RCarrée(h(Rhoeau +RhoHg)) - RCarrée((Rhoeau.h + RhoHg.z))](de 0àh)
T1 = S/s * Rcarrée(2/(g.RhoHG)) * [RCarrée(h(Rhoeau +RhoHg)) - RCarrée(Rhoeau.h)]
*****
... Et puis il reste à calculer la durée T2 de la vidange d'eau seule ... ce qui devrait être immédiat en remplaçant RhoHg par Rhoeau et Rhoeau par 0 dans la formule de T1
T2 = S/s * Rcarrée(2/(g.Rhoeau)) * [RCarrée(h(Rhoeau))]
T2 = S/s * Rcarrée(2h/g)
*****
Durée totale de vidange : T = T1 + T2 = ...
Aucun calcul vérifié (à faire évidemment).
Bonjour
Je crois que JP oublie de tenir compte du coefficient de contraction du jet, noté "m" ici . Comme l'a noté nano21 dans son message du 25-12-17 à 13:13 :
Qv = m. (VB) . S
Un peu plus de détail ici : 
(paragraphe sur : vidange d'un réservoir - formule de Torricelli)
Oui, je n'avais même pas vu que c'était mentionné.
Enfin, c'est immédiat de l'introduire dans le raisonnement.
je vous remercie beaucoup Vanoise et J-P pour votre aide......
Donc le temps nécessaire pour vidanger le réservoir sera:
T=S/m.s [2/gHg(
eau.h-Hg.h)-eau.h)+(2h/g)]
Annuler
connectez vous