Inscription / Connexion Nouveau Sujet
Le T.M.C
Bonjour à tous !!
Alors voilà je me suis lancée dans un exercice mais je rencontre quelques difficultés. Je vais mettre l'énoncé et ce que j'ai fait.
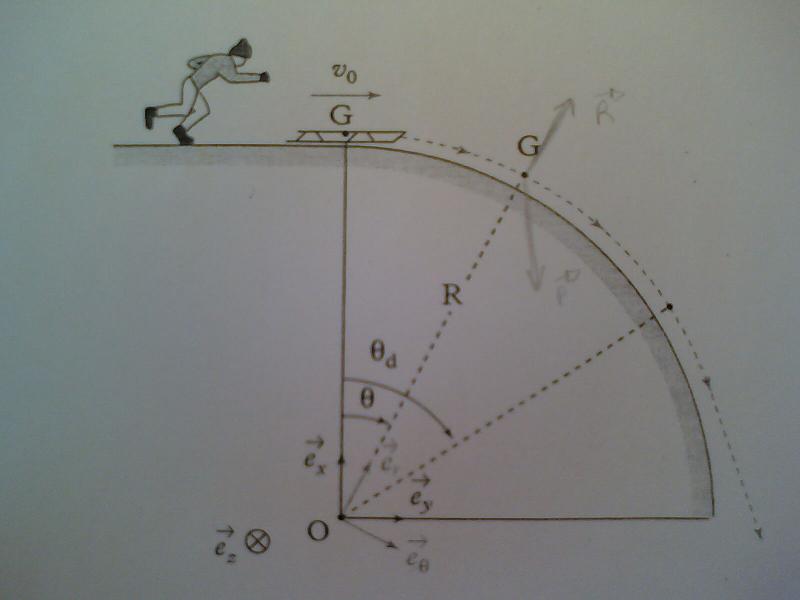
Une luge assimilée à un point matériel G de masse m arrive au niveau d'un profil circulaire avec une vitesse horizontale v0. Tant que la luge suit ce profil, elle décrit une trajectoire circulaire de rayon R=5m et est repérée par l'angle 
. On néglige tous les frottements. Le réferentiel Rg (o;ex,ey,ez) lié à la Terre est supposé galiléen.
1) Ecrire l'équation différentielle du mouvement à l'aide du TMC
2) En déduire l'expression de . en fonction de et de v0.
3) A l'aide d'une autre équation de la dynamique, donner l'expression de la réaction du sol.
4) En déduire l'angle d à partir duquel la luge quitte le profil circulaire (en fonction de v0)
Jusqu'ici, je n'ai réussi à faire que la 1)
d(
o(G))/dt = 
Mo(Fi)
= Mo(P) + Mo(R)
Mo(P) = OG 
P
= (R er) (mg ex)
= Rmg sin ez
Mo(R) = OG R
= 0
car OG et R sont colinéaires
o(G) = OG P
= (R er) (mv)
= (R er) m(R.er+ R.e)
= mR2. ez
D'où:
d(mR2. ez) / dt = Rmg sin ez
mR2.. = Rmg sin
.. - g/R = 0
Merci d'avance à ce qui pourront m'aider !!
Bonjour merci de m'avoir répondu.
ChateauDav, je ne vois pas très bien comment tu arrive à .0 = Cte = v0/R. Peut-tu m'expliquer ...
Merci d'avance.
Tu prends la relation précédente et tu fais théta=0, car c'est la valeur de théta à l'instant initial.
Donc tu as Théta point = Cte
Comment trouver la valeur de cette constante ?
Tu sais que : théta point = oméga (vitesse angulaire) = v/R
ok ok oui c'est vrai que ça tombe sous le sens, c'était juste devant mes yeux et je ne l'ai pas vu !!!
merci
Bon voilà, j'ai trouvé la question 2) . = (2v0 - g2)/2R
Ensuite pour la question 3) j'ai utilisé le PFDLD
F =ma
J'ai utilisé les coordonnées cylindro-polaires et j'ai projetté sur er
m(R..-R. 2)er = (N-Rcos)er
-mR. 2 = N-Rcos
N=R(cos-m. 2)
J'aimerais savoir si déjà jusque là c'est bon.
Merci
Force tangentielle due au poids : F = m.g.sin(theta)
Couple = m.g.R.sin(theta) = m.R².d²theta/dt²
m.R².d²theta/dt² = m.g.R.sin(theta)
d²theta/dt² = (g/R).sin(theta)
d(dtheta/dt)/dt = (g/R).sin(theta)
d(dtheta/dt)/dtheta * dtheta/dt = (g/R).sin(theta)
d(dtheta/dt) * (dtheta/dt) = (g/R).sin(theta) dtheta
On intègre :
(1/2).(dtheta/dt)² = -(g/R).cos(theta) + K1
(dtheta/dt)² = -2.(g/R).cos(theta) + K2
Or N = m(g.cos(theta) - R.(dtheta/dt)²)
--> N = m(g.cos(theta) + R.2.(g/R).cos(theta) + K3)
N = mg.(cos(theta) + 2.cos(theta) + K)
N = mg.(3.cos(theta) + K)
en theta = 0, N = mg - m.vo²/R
--> mg - m.vo²/R = mg.(3.cos(0) + K)
1 - vo²/(gR) = (3 + K)
K = -2 - vo²/(gR)
N = mg.(3.cos(theta) - 2 - vo²/(gR))
Décollage pour N = 0 --> si : 3.cos(theta_d) - 2 - vo²/(gR) = 0
cos(theta_d) = (vo²/(gR) + 2)/3
cos(theta_d) = (vo² + 2gR)/(3gR)
theta_d = arcos[(Vo² + 2.gR)/(3.R.g)]
----------
Autre méthode (différente de celle demandée, mais plus directe).
Conservation de l'énergie mécanique de la luge :
(1/2).m.Vo² + m.g.R(1-cos(theta)) = (1/2).m.V²
Vo² + 2.g.R(1-cos(theta)) = V²
F centrifuge = m.v²/R = (m/R).[Vo² + 2.g.R(1-cos(theta))]
Composante axiale du poids = P.cos(theta) = m.g.cos(theta)
Réaction du sol : N = m.g.cos(theta) - (m/R).[Vo² + 2.g.R(1-cos(theta))]
Quitte la piste lorsque N = 0, donc pour :
m.g.cos(theta_d) = (m/R).[Vo² + 2.g.R(1-cos(theta_d))]
R.g.cos(theta_d) = [Vo² + 2.g.R(1-cos(theta_d))]
3.R.g.cos(theta_d) = (Vo² + 2.g.R)
cos(theta_d) = (Vo² + 2.g.R)/(3.R.g)
theta_d = arcos[(Vo² + 2.g.R)/(3.R.g)]
-----
Sauf distraction ou erreur. 
Annuler
connectez vous