Inscription / Connexion Nouveau Sujet
le principe fondamental de la dynamique
Bonjour
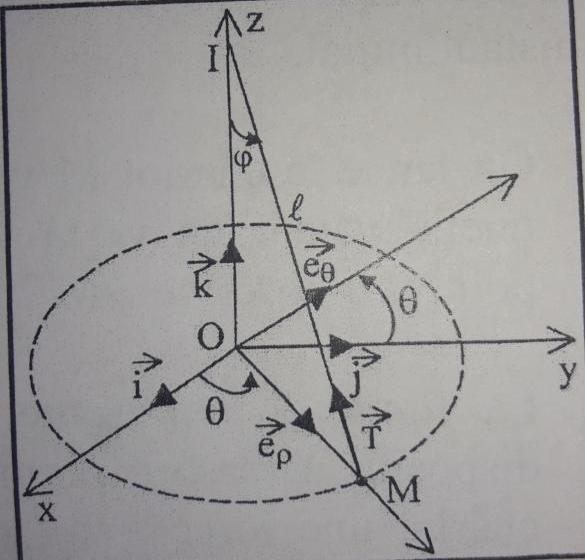
Considérons un pendule en mouvement de rotation uniforme, de vitesse angulaire w=cste=  par rapport à un référentiel galiléen R=(O,x,y,z) = (O,
par rapport à un référentiel galiléen R=(O,x,y,z) = (O, ,
, ,
, ) . le pendule est constituée d'un point matériel M de masse m suspendu en un point fixe I de l'axe Oz par un fil inextensible sans masse et de longueur L . soit
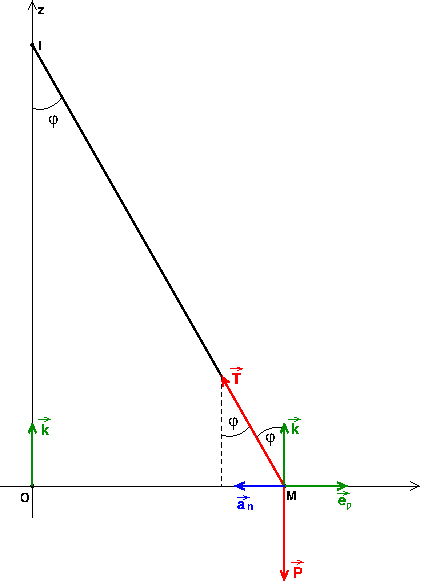
) . le pendule est constituée d'un point matériel M de masse m suspendu en un point fixe I de l'axe Oz par un fil inextensible sans masse et de longueur L . soit  l'angle que fait le fil de suspension avec la verticale IO ( voir figure ) . On appelle T la tension du fil .
l'angle que fait le fil de suspension avec la verticale IO ( voir figure ) . On appelle T la tension du fil .
a) en appliquant le PFD , trouver une relation entre w ,  , L et g ( g étant la pesanteur de la terre ) . En déduire la période de rotation T' et la vitesse angulaire minimale de rotation w0 pour que l'on puisse observer la déviation sous l'angle
, L et g ( g étant la pesanteur de la terre ) . En déduire la période de rotation T' et la vitesse angulaire minimale de rotation w0 pour que l'on puisse observer la déviation sous l'angle  .
.
j'ai bloqué dans la 1er question
je voudrais votre aide
Bonjour
Il suffit d'appliquer la relation fondamentale de la dynamique et de projeter suivant les axes dirigés par les vecteurs j et e .
.
Évidemment, cela suppose de connaître l'expression de l'accélération d'une masse ponctuelle en mouvement circulaire uniforme.
J'ai mal pris en compte ton schéma : il faut projeter la relation fondamentale de la dynamique suivant les vecteurs k et e . Tu as tout intérêt à faire une figure en 2D dans le plan contenant les points O, I et M. Tu peux éventuellement la scanner et la poster ici.
. Tu as tout intérêt à faire une figure en 2D dans le plan contenant les points O, I et M. Tu peux éventuellement la scanner et la poster ici.
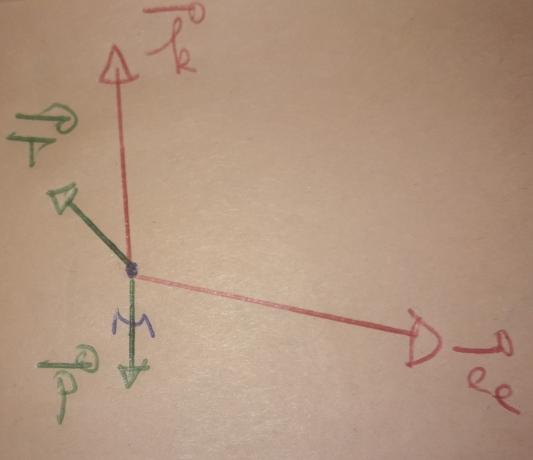
Refais le schéma comme conseillé. Tu remarqueras que les vecteurs force et le vecteur accélération s'expriment simplement en fonction de ces deux vecteurs unitaires.
Non : les deux vecteurs unitaires sont perpendiculaires. Pour bien comprendre, il faut dessiner le fil, placer le point I et représenter l'angle  .
.
Très bien !
Projėte maintenant la relation fondamentale de la dynamique sur l'axe horizontal et l'axe vertical.
Maintenant : que vaut le vecteur accélération du point M sachant que son mouvement est circulaire et uniforme de rayon :
R=OM=l.sin( ) ?
) ?
Bonjour,
Inutile de faire des scans pour les propositions de réponse, le forum a tout ce qu'il faut :
je pense on aure deux accélérations
normale et tangentielle non ?
Dans le cas général oui mais ici le mouvement est circulaire et uniforme (vecteur vitesse de norme constante). L'accélération tangentielle est nulle. Reste donc l'accélération normale à prendre en compte...
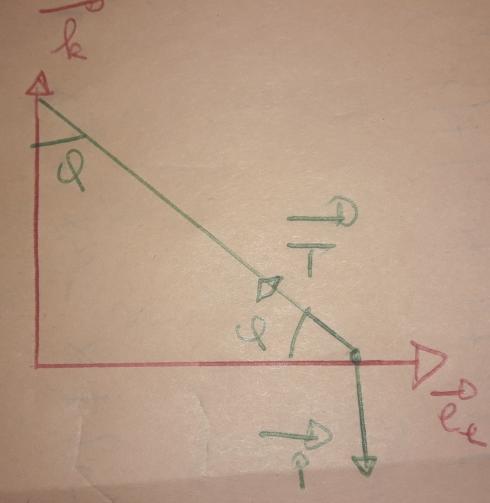
J'ai laissé hier soir passer une erreur sur ton schéma. L'angle  , selon l'énoncé, est l'angle au sommet I. Sauf cas particulier (
, selon l'énoncé, est l'angle au sommet I. Sauf cas particulier ( =45°), l'angle au sommet M du triangle rectangle est différent, il s'agit du complémentaire de
=45°), l'angle au sommet M du triangle rectangle est différent, il s'agit du complémentaire de  .
.
J'ai laissé hier soir passer une erreur sur ton schéma. L'angle
 , selon l'énoncé, est l'angle au sommet I. Sauf cas particulier (
, selon l'énoncé, est l'angle au sommet I. Sauf cas particulier ( =45°), l'angle au sommet M du triangle rectangle est différent, il s'agit du complémentaire de
=45°), l'angle au sommet M du triangle rectangle est différent, il s'agit du complémentaire de  .
.qu'est ce que je dois modifier maintenant ?
Oui ; ce vecteur étant centripète et non centrifuge :
Tu peux maintenant projeter la relation vectorielle correspondant à la relation fondamentale de la dynamique dans la base .
Cela a déjà dit mais il est peut-être utile de rappeler que, puisque le mouvement de M est uniforme, son accélération tangentielle est nulle. L'accélération de M se confond donc avec son accélération normale.

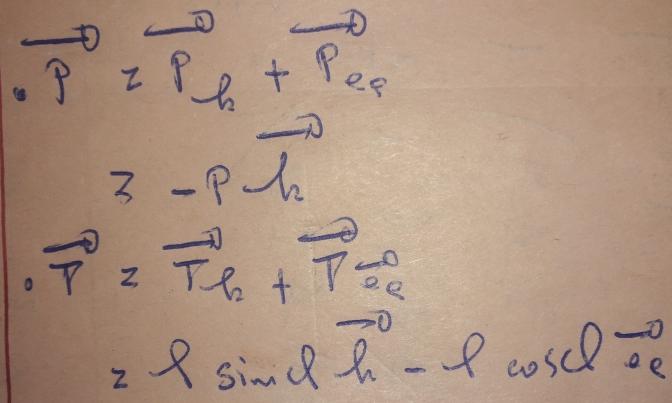

 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum