plllllllllllllllz
aidez moi

Bonjour,

Pour le premier point :



Le point en bleu
Le rectangle d'incertitude en rouge

Bonjour mohibe18, et bonjour Coll

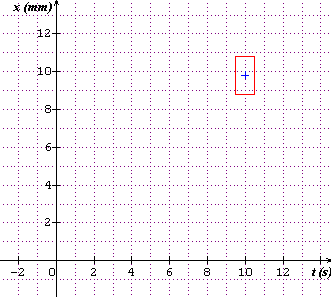
J'avais préparé hier une figure pour répondre à ce topic, permettez-moi de la mettre ci-dessous car elle complète très bien celle de Coll :

mobibe, un rectangle d'erreur est un rectangle dont le centre est le point de mesure (t1, x1) et dont les côtés ont pour longueur 2t et 2x : ainsi, tous les points enfermés dans ce rectangle ont des coordonnées t et x telles que t₁ - t t t₁ - t et x₁ - x x x₁ - x, donc ils constituent des résultats possibles pour cette mesure, aux incertitudes près. OK ?

Les questions que je me pose sont celles-ci :
a)  puisque l'erreur de lecture sur le réglet vaut 1 mm, pourquoi donner les mesures de x en mm et avec une décimale ?
b)  puisque l'erreur sur la mesure au chronomètre vaut 0,5 s, pourquoi donner les mesures de t en seconde mais sans décimale ?
c) pour mesures une distance avec une règle, il faut deux mesures : celle de l'origine et celle de l'extrémité du segment qu'on veut mesurer. Peut-être faut-il doubler la valeur de l'erreur de lecture sur le réglet et écrire x = 2 mm ; même remarque pour la mesure du temps au chronomètre, car il y a un déclenchement pour le mettre en route et un déclenchement pour l'arrêter, donc deux fois l'erreur due au reflexe du manipulateur ; soit t = 1 s.

Qu'en penses-tu, Coll ?

erratum : au c), lire pour obtenir une distance avec une règle...

Bonjour,

Pour information, le sujet a été également abordé dans le forum de l'île des maths...  (Lien cassé)
C'est d'ailleurs moi qui l'ai orienté vers l'île de la Physique, plus indiquée pour son sujet...

En l'occurrence, mohibe18 ne comprenait pas pourquoi    et    sont simplement constants dans cet exercice...
... et pourquoi ils peuvent ne pas l'être dans d'autres situations.

Bonjour LeDino,

merci pour cette info. Le problème des incertitudes de mesure en sciences expérimentales, surtout en physique, est bien plus complexe qu'il n'y paraît, et les collègues avec lesquels j'ai travaillé tout le long de ma carrière ne sont pas toujours d'accord quand il s'agit de déterminer l'incertitude sur une mesure directe. Je garde le souvenir de quelques belles empoignades... Je ne peux pas répondre à mohibe18 sur ce point, pour la raison que, en effet, cela dépend de la situation (type de mesure, appareil utilisé, mesures répétitives et valeur moyenne etc...).

Merci d'avoir réagi et de nous avoir informés, Coll et moi-même.

Prbebo.

Bonsoir prbebo et LeDino

Les incertitudes de mesure ! !

Je ne connais qu'un texte correct sur le sujet : le "GUM"
En France, les professeurs de physique de maths-sup et maths-spé ont été formés... Des professeurs de "grandes écoles" ont été formés... mais...

La méthode décrite est d'application obligatoire pour les laboratoires de métrologie nationaux (et en particulier pour les comparaisons internationales qui sont l'un des piliers de la métrologie appliquée).

Bonsoir Coll,

je ne connaissais pas ce texte ; je viens de télécharger l'archive et je vais regarder ça ce soir avec intéret, surtout s'il fait force de loi en métrologie. A Lille nous nous sommes finalement mis d'accord sur le livre de John Taylor, "incertitudes et analyse des erreurs dans les mesures physiques", chez Dunod. Traduction française parue en 2000. C'est le seul ouvrage à ma connaissance qui explique clairement pourquoi, lorsqu'on additionne des mesures indépendantes, l'incertitude sur cette somme se calcule en faisant la somme quadratique des incertitudes sur chaque terme de la somme. Voir ici pour les références, et ici pour l'avis des internautes...

Bonne soirée et à bientôt sur le forum.  BB.

L'indépendance des mesures étant elle aussi en soi un sujet à part entière ...
Si une part de l'erreur provient d'un biais systématique, il n'y a pas d'indépendance sur cette part.

L'incertitude sur la correction (probablement imparfaite) d'une erreur systématique induit en effet des corrélations...

Merci prbebo pour cette référence que je ne connais pas.
Étant donnée la date de traduction en français, il est possible que l'original américain soit conforme à la première édition du GUM.
Amusant de constater que le nom de l'auteur est homonyme de celui qui fut l'un des grands rédacteurs du GUM (Barry N. Taylor du NIST), probablement à la retraite maintenant.