Inscription / Connexion Nouveau Sujet
lancement projectile
Bonjour, je bloque entièrement sur un exo:
"Un canon est situé sur une colline représentée par un plan incliné faisant un angle avec l'horizontale.
on lance un projectile vers le haut dans une direction faisant un angle avec la colline.
Calculer pour que le projectile ait une vitesse horizontale lorsqu'il touche la colline.
Réponse:
Je n'arrive pas à traduire l'énoncé.
Pourriez vous me donner des indices?
Merci !
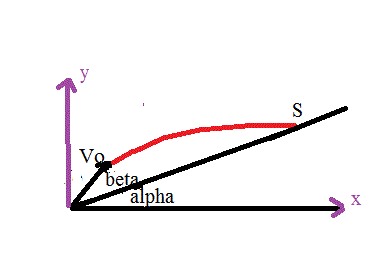
Dans le repère dessiné :
Pour le projectile :
x = Vo.cos(alpha+beta).t
y = Vo.sin(alpha+beta).t - gt²/2
vx = Vo.cos(alpha+beta)
vy = Vo.sin(alpha+beta) - gt
----
Vitesse horizontale pour vy = 0, soit pour Vo.sin(alpha+beta) - gt = 0
Donc à l'instant : t1 = (Vo/g).sin(alpha+beta)
A cet instant le projectile est en S(Vo.cos(alpha+beta).t1 ; Vo.sin(alpha+beta).t - gt1²/2)
Soit donc, après calculs : S(Vo²/g .cos(alpha+beta).sin(alpha+beta) ; Vo²/(2g) * sin²(alpha+beta))
----
La trace de la colline dans le repère est la droite OS d'équation: y = tg(alpha) * x
--> Vo²/(2g) * sin²(alpha+beta) = tg(alpha) * Vo²/g .cos(alpha+beta).sin(alpha+beta)
sin(alpha+beta) = 2 tg(alpha).cos(alpha+beta)
tg(alpha+beta) = 2 tg(alpha)
(tg(alpha) + tg(beta))/(1 - tg(alpha).tg(beta)) = 2 tg(alpha)
tg(alpha) + tg(beta) = 2.tg(alpha) - 2.tg²(alpha).tg(beta)
tg(beta) = tg(alpha) - 2.tg²(alpha).tg(beta)
tg(beta) * (1 + 2.tg²(alpha)) = tg(alpha)
tg(beta) = tg(alpha)/(1 + 2.tg²(alpha))
-----
Sauf distraction. 


