Inscription / Connexion Nouveau Sujet
Lampe au néon Circuit linéaire du 1er ordre
Bonsoir à vous, jai une question à un exo qui me pose problème.
Voici l exercice :
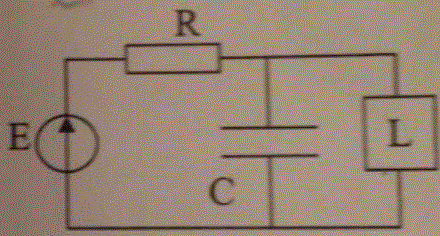
L est une lampe au néon de tension d allumage Va = 90 V et Vb= 70 V. Lorsque la lampe est éteinte sa résistance peut être considérée comme infinie. Lorsque elle est allumée sa résistance prend la valeur r=10000 ohm. Le circuit est joint à ce message.
Voilà mon soucis, la question que je n'ai pas réussi à résoudre, la premiere de mon exo, est la suivante : je dois justifier qualitativement le fait que la lampe émette des flashs.
Je sais ce qu'est une étude qualitative mais je ne vois pas du tout comment je peut trouver, Ca fait pas mal de telles que je suis bloque, j'espère avoir de l aide 
Merci d avance !!
** image supprimée **
Pour que cela fonctionne, il faut avoir 90 < E < 140 (en volts) et il faut que R aie une valeur telle que 10000.E/(R + 10000) < 70
Si ces conditions sont respectées (lacunes de l'énoncé qui ne les a pas données) :
Le néon étant éteint, sa résistance est infinie.
Le condensateur se charge à travers la résistance R, la tension "grimpe" vers E.
Lorsque la tension aux bornes de C (donc aux bornes du néon) atteint 90 V, le néon s'allume et son courant décharge le C.
La tension sur C (donc aussi sur le néon en parallèle) redescend vers une tension égale à 10000.E/(R + 10000) et lorsqu'elle atteint 70 V, le néon s'éteind ... et on est revenu à la situation initiale.
Donc le cycle se poursuit.
Sauf distraction. 
1°
Néon éteint et u(0) = 70 V comme condition initiale.
Avec u la tension sur C :
(E-u)/R = C.du/dt
RC.du/dt + u = E
u(t) = E + K1.e^(-t/(RC))
u(0) = 70 --> 70 = E + K1 ; K1 = 70 - E
u(t) = E + (70 - E).e^(-t/(RC))
Ceci jusque u = 90 V (lorsque le néon s'allume)
Soit t1 la durée de néon éteint, on a : E + (70 - E).e^(-t1/(RC)) = 90
e^(-t1/(RC)) = (90 - E)/(70 - E)
t1 = RC.ln((70-E)/(90-E)) (durée néon éteint)
-----
2°)
Néon allumé (on remet l'origine d'horloge à l'instabnt où le néon s'allume) --> u(0) = 90 (V)
(E - u)/R - u/r = C.du/dt
R.r.C.du/dt + (R+r).u = E/R
u(t) = E * R/(R+r) + K2.e^(-t.(R+r)/(R.r.C))
u(0) = 90 --> 90 = E * R/(R+r) + K2
K2 = 90 - E*R/(R+r)
u(t) = E * R/(R+r) + (90 - E*R/(R+r)).e^(-t.(R+r)/(R.r.C))
Ceci jusque u = 70 V (lorsque le néon s'éteint)
Soit t2 la durée de néon allumé, on a : E * R/(R+r) + (90 - E*R/(R+r)).e^(-t2.(R+r)/(R.r.C)) = 70
e^(-t2.(R+r)/(R.r.C)) = (70 - E * R/(R+r))/(90 - E*R/(R+r))
t2 = R.r.C/(R+r) * ln((90 - E*R/(R+r))/(70 - E*R/(R+r))) (durée néon allumé)
-----
La période T du cycle est T = t1 + t2
... et rappel de ma réponse précédente (que je corrige, car j'avais cru voir R = 10000 ohms aussi) , pour que cela fonctionne il faut que :
E > 90 V et il faut que R aie une valeur telle que r.E/(R + r) < 70
----------
Calculs non vérifiés.
Sauf distraction. 


