Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Lames infinies uniformément chargées- Électrostatique

Posté par
nico10310 30-10-17 à 11:12

Bonjour,

Voici mon sujet :

On considère une lame infinie d'épaisseur d uniformément chargée de densité volumique de charge ρ > 0, perpendiculaire à l'axe (Oz). On souhaite déterminer le champ électrostatique créé par la lame en tout point de l'espace (à l'intérieur comme à l'extérieur de la lame). (cf shéma)

Question 1 : Par des considérations de symétrie et d'invariance, déterminer la direction du champ électrostatique \vec{E}  en un point M quelconque et les variables dont il peut dépendre. Que peut on dire du champ électrique au point O Comparer le champ électrostatique au point d'ordonnée z > 0 et à son symétrique d'ordonnée (−z).

Question 2 : Énoncer le théorème de Gauss.

Question 3 : En appliquant le théorème de Gauss sur une surface judicieusement choisie, déterminer le champ électrostatique \vec{E} en tout point.

Question 4 : On considère maintenant une deuxième lame d'épaisseur d uniformément chargée avec une densité volumique de charge ρ' et parallèle à première lame. Cette deuxième lame est placée dans le demi-espace supérieur (z > 0) à une distance D de la première lame avec D > d. En utilisant les résultats de questions précédentes, déterminer le champ électrostatique dans l'espace entre les deux lames (pour un
point d'ordonnée z telle que d/2 < z < D − d/2) dans les cas suivants :
a) les lames ont des densités volumique de charge identiques ρ' = ρ
b) les lames ont des densités volumique de charge opposées ρ' = −ρ.


Et mes réponses :

1) (xOy) est un plan de symétrie. Il y a une infinité de plans de symétries parallèles au plan (xOz). Donc \vec{E} ne dépend que de z. On a \vec{E}(O)=0 et \vec{E}(z)=\vec{E}(-z)
Est-ce correct ?

2) Th de Gauss : \phi _{\vec{E}}=\oint_{}^{}{\oint_{S}^{}{\vec{E}\vec{n}dS}}=\frac{Q_i_n}{\epsilon _0}

3) J'ai pris un parallélépipède à base carré (cf mon schéma)
Je tape ma réponse sur Word afin que ça soit plus simple :
schéma :

calculs :

Je trouve donc un champ électrostatique nul. Est-ce possible ? Est ce qu'il faut que je prenne une autre surface hors de la plaque ?

Merci pour vos réponses

Lames infinies uniformément chargées- Électrostatique

Posté par
vanoisere : Lames infinies uniformément chargées- Électrostatique 30-10-17 à 17:39

Bonjour

Tu démarres bien : pas de problème pour les généralités sur les symétries, les invariances et le choix de la surface de Gauss. Pas d'accord sur les résultats. Le flux à travers le parallélépidède rectangle de base d'aire S et de demie hauteur z vaut simplement :

\Phi=2.E_{(z)}.S=\frac{Q_{int}}{\varepsilon_{0}}\quad;\quad E_{(z)}=\frac{Q_{int}}{2\varepsilon_{0}.S}

Premier cas : 0<z<d/2 :

Q_{int}=\rho.S.2z : charge contenue dans le parallélépipède rectangle de hauteur 2z.

E_{(z)}=\frac{\rho.z}{\varepsilon_{0}}

Deuxième cas : z>d/2 :

Q_{int}=\rho.S.d

E_{(z)}=\frac{\rho.d}{2\varepsilon_{0}}

Les situations z<0 se déduisent par symétrie. Mes indications sont un peu succinctes. N'hésite pas à poster à nouveau si tu ne comprends pas bien.
Je te laisse continuer...

Posté par
nico10310re : Lames infinies uniformément chargées- Électrostatique 31-10-17 à 13:56

vanoise @ 30-10-2017 à 17:39



Tu démarres bien : pas de problème pour les généralités sur les symétries, les invariances et le choix de la surface de Gauss. Pas d'accord sur les résultats. Le flux à travers le parallélépidède rectangle de base d'aire S et de demie hauteur z vaut simplement :

\Phi=2.E_{(z)}.S=\frac{Q_{int}}{\varepsilon_{0}}\quad;\quad E_{(z)}=\frac{Q_{int}}{2\varepsilon_{0}.S}


Merci, mais je ne comprends pas pourquoi \Phi=2.E_{(z)}.S
Comment est ce que mon  parallélépipède rectangle est placé sur la figure ?

Posté par
Pikimidbre : Lames infinies uniformément chargées- Électrostatique 01-11-17 à 12:21

Salut,

Je crois qu'il y a une erreur dans ton résultat \vec{E}(z)=\vec{E}(-z) , c'est plutôt -\vec{E}(z)=\vec{E}(-z) (regarde ton schéma) d'où le résultat de Vanoise.

Posté par
nico10310re : Lames infinies uniformément chargées- Électrostatique 02-11-17 à 10:32

Pikimidb @ 01-11-2017 à 12:21

Salut,

Je crois qu'il y a une erreur dans ton résultat \vec{E}(z)=\vec{E}(-z) , c'est plutôt -\vec{E}(z)=\vec{E}(-z) (regarde ton schéma) d'où le résultat de Vanoise.


Oui effectivement, merci

Posté par
nico10310re : Lames infinies uniformément chargées- Électrostatique 02-11-17 à 11:29

J'ai réussi à corriger mon erreur sur le calcul du flux, mais maintenant je ne comprends pas ces 2 cas :

vanoise @ 30-10-2017 à 17:39


Premier cas : 0<z<d/2 :

Q_{int}=\rho.S.2z : charge contenue dans le parallélépipède rectangle de hauteur 2z.

E_{(z)}=\frac{\rho.z}{\varepsilon_{0}}

Deuxième cas : z>d/2 :

Q_{int}=\rho.S.d

E_{(z)}=\frac{\rho.d}{2\varepsilon_{0}}


Je sais que Q_{int}=\rho V pourquoi prendre un volume de S2z ?

Merci

Posté par
vanoisere : Lames infinies uniformément chargées- Électrostatique 02-11-17 à 12:08

Premier cas : le parallélépipède est entière ment inclus dans la lame épaisse
Dans le second cas, les charges sont présentes seulement sur l'épaisseur d ; fais un schéma si cela ne te parait pas évident...

Posté par
LordOfLambsre : Lames infinies uniformément chargées- Électrostatique 02-11-17 à 17:28

Bonjour,
Je trouve les mêmes résultats que vous. mais n'est il pas étrange que le champ pour le second cas ne dépend pas de z ?

Posté par
vanoisere : Lames infinies uniformément chargées- Électrostatique 02-11-17 à 17:59

Bonsoir LordOfLambs

Citation :
mais n'est il pas étrange que le champ pour le second cas ne dépend pas de z ?

Cela semble effectivement défier le sens commun ! Tout simplement parce que dans la réalité, une plaque uniformément chargée de dimensions infinie : cela n'existe pas ! Cette modélisation est cependant traitée en cours de physique car elle constitue une bonne approximation de la situation correspondant à une plaque réelle de dimensions finies lorsque le point M où on étudie le champ est à une distance de la plaque très petite devant la longueur et la largeur de la plaque, le point M étant éloigné des bords de la plaque.
Sans vouloir trop anticiper la suite de l'exercice : deux plaques parallèles possédant des charges opposées : cela fait penser au condensateur et on admet couramment que le champ électrique entre les plaques est uniforme sauf au voisinage des bords des plaques...

Posté par
nico10310re : Lames infinies uniformément chargées- Électrostatique 02-11-17 à 20:41

vanoise @ 02-11-2017 à 12:08

Premier cas : le parallélépipède est entière ment inclus dans la lame épaisse


Oui d'accord pour le 1er cas, c'est parce que la hauteur du parallelepipede est 2z mais ne pourrait on pas prendre z ?

Et pour le 2e cas, le parallelepipede est toujours dans la lame ? Si oui c'est bon j'ai compris.

Posté par
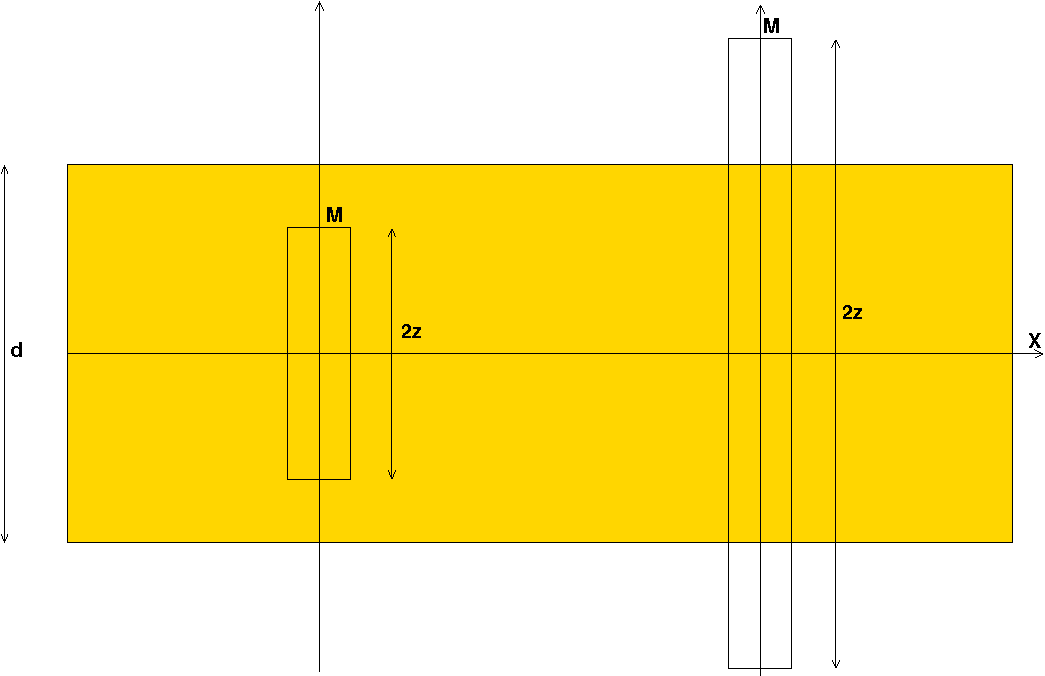
vanoisere : Lames infinies uniformément chargées- Électrostatique 02-11-17 à 21:07

Le schéma ci-dessous (coupe par un plan perpendiculaire à la plaque épaisse chargée) devrait t'aider.
Dans le premier cas (gauche sur la figure), le parallélépipède de Gauss est entièrement dans la lame épaisse ; la hauteur du parallélépipède à prendre en compte pour le calcul de la charge intérieure est donc la hauteur totale du parallélépipède : 2z
Dans le second cas (à droite sur la figure), le parallélépipède de Gauss ne contient des charges que sur une hauteur d...

Lames infinies uniformément chargées- Électrostatique

Posté par
nico10310re : Lames infinies uniformément chargées- Électrostatique 03-11-17 à 11:19

Ah oui d'accord, merci beaucoup !

Et donc pour les situations z<0, il suffit de prendre l'opposé des expressions obtenues :
donc si   -d/2 < z < 0, E_z=-\frac{\rho z}{\epsilon _0} et si z < -d/2,  E_z=-\frac{\rho d}{2\epsilon _0}

Question 5 :
Pour la plaque du haut,  si   z < D + d/2, on a de la même manière E_z=-\frac{\rho' d}{2\epsilon _0}
Donc en prenant en compte la plaque du bas, si d/2 < z < d/2 + D, on a E_z=\frac{\rho d}{2\epsilon _0}-\frac{\rho' d}{2\epsilon _0}

Ainsi :
- si \rho =\rho ' alors E_z=0
- si \rho '=-\rho alors E_z=2\frac{\rho d}{2\epsilon _0}=\frac{\rho d}{\epsilon _0}

Est-ce correct ?
Merci

Posté par
vanoisere : Lames infinies uniformément chargées- Électrostatique 03-11-17 à 12:36

Parfait !

Posté par
nico10310re : Lames infinies uniformément chargées- Électrostatique 03-11-17 à 13:41

Merci !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !