Inscription / Connexion Nouveau Sujet
Lame et miroir
Bonsoir,
A) On considère un dioptre plan horizontal séparant l'air et un milieu d'indice n.
Un rayon lumineux dans l'air rencontre le dioptre avec angle d'incidence et se propage dans le second milieu d'indice n avec un angle de réfraction
1) Calculer l'indice de réfraction n du second milieu de propagation.
2) Quelle est la vitesse V de la lumière dans ce milieu sachant qu'elle se propage à la vitesse C0 = 3.108 m/s dans l'ar ?
B) On place un second dioptre plan parallèle au premier et séparé se celui-ci de la distance e. On définit ainsi, une lame à faces parallèles d'épaisseur e et d'indice n placé dans l'air.
3) Faire un schéma indiquant la marche d'un rayon lumineux et son déplacement laléral à travers la lame.
4) Déterminer l'expression du déplacement latéral du rayon lumineux en fonction de e,
et
.
5)Que devient cette expression pour un rayon paraxial ?
C) Sur la face inférieure de la lame, on passe une couche de peinture noire ; celle-ci devient alors un miroir plan. Le système optique ainsi obtenu est un miroir commercial (voir la figure ci-dessous).
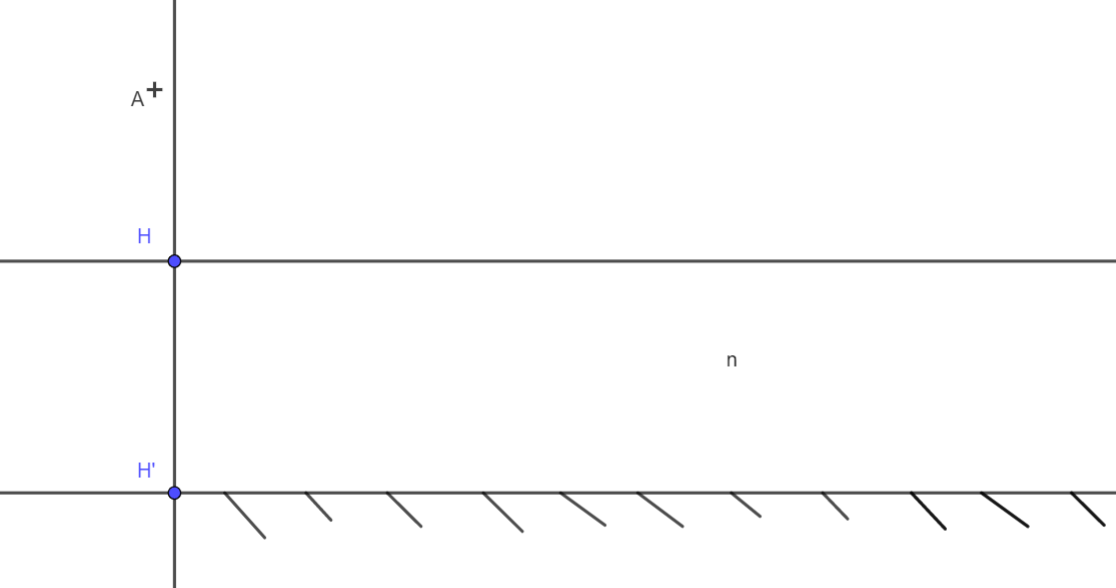
6) Déterminer graphiquement la position de l'image A' de l'objet A donnée par ce nouveau système.
On indiquera également la position dechaque image intermédiaire.
7) Donner les différentes conjugaison (objet-image) ainsi que les formules de conjugaisons associées.
Je bloque sur la 3e question..
Bonsoir
Pour la question 3, le paragraphe 3.1 de ce document devrait t'aider. N'hésite pas à poser des questions complémentaires si tu le juges utile.
La démonstration est faite sur le document que je t'ai indiqué. Il faut juste adapter les notations.
5) Expression du déplacement pour un rayon paraxial.
Pour un rayon paraxial c'est-à-dire lorsque
Dois-je remplacer par
dans cette expression du déplacement ?
Rayon paraxial dans ce contexte : les angles 
et 
sont suffisamment petits pour autoriser un développement limité au premier ordre des fonctions trigonométriques :
sin()
; sin() ; sin(-)- ;
cos()1 ; cos()1 ;
on aurait de même : tan() et ainsi de suite mais cela n'intervient pas dans cet exercice.
Ainsi, la loi de Descartes sur la réfraction conduit à une relation très simple entre et .
Loi de Descartes pour la réfraction :
sin()=n.sin().
Pour les angles petits :
=n..
D'où simplification de ton expression.
Je ne vois pas de réponse à la question 6. La méthode générale est la suivante.
Tu considère un point objet réel A dans l'air. Tu détermines son image A1 par le dioptre plan (voir cours correspondant et formule de conjugaison valide pour rayons peu écartés de la normale (rayons paraxiaux)). Ensuite, tu considère que l'image définitive A' de A est l'image par le miroir plan de A1.
Cette question est difficile à traiter sans un cours structuré sur la notion de stigmatisme, d'objet et d'image...Tu peux éventuellement t'aider de ce document, parties 1 et 2.
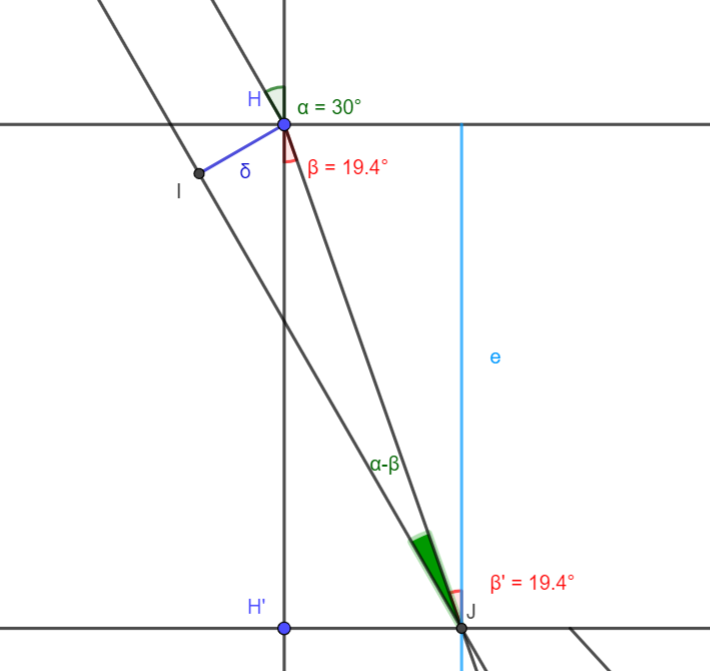
Peut-être une question d'habitude mais je préfère tracer horizontalement la normale à la lame et au miroir.
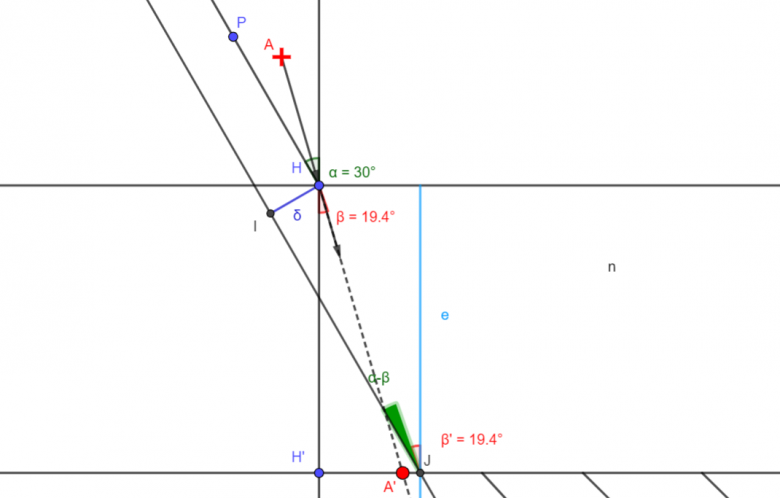
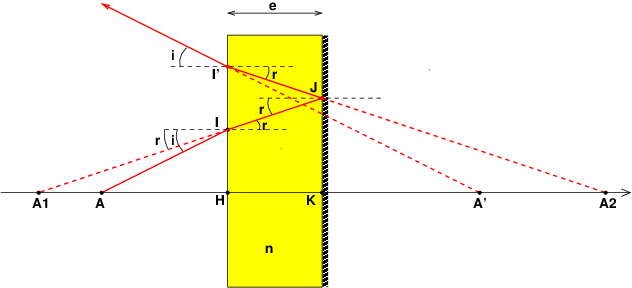
Soit un point A objet réel donc supposé émettre des rayons paraxiaux. Cas particulier simple : le rayon émis sous incidence normale se réfléchit sur lui-même sans déviation : conclusion : l'image A' de A sera nécessairement sur cette normale.
On trace alors un autre rayon incliné par rapport à la normale d'un angle "i" supposé petit (pour plus de clarté, je l'ai fortement exagéré sur le schéma). Le rayon incident est réfracté . Le rayon réfracté IJ semble venir de A1 : image virtuelle de A par le dioptre plan.
Ce rayon se réfléchit en J en semblant provenir d'un point A2, symétrique de A1 par rapport au plan du miroir passant par K.
Le rayon réfléchit JI' subit une réfraction en I dont le prolongement est le point A' : image virtuelle de l'objet réel A par l'ensemble {dioptre , miroir).
Je te laisse réfléchir à tout cela et mettre la situation en équations. Je vais être franc : comprendre cet exercice suppose d'avoir compris le cours sur la notion d'objet et d'image, réels ou virtuels...
Les formules de conjugaison sont démontrées sur le document que je t'ai indiqué dans mon message du 18-02-22 à 23:08.
Annuler
connectez vous