Inscription / Connexion Nouveau Sujet
Lagrangien d'un systeme
bonjour
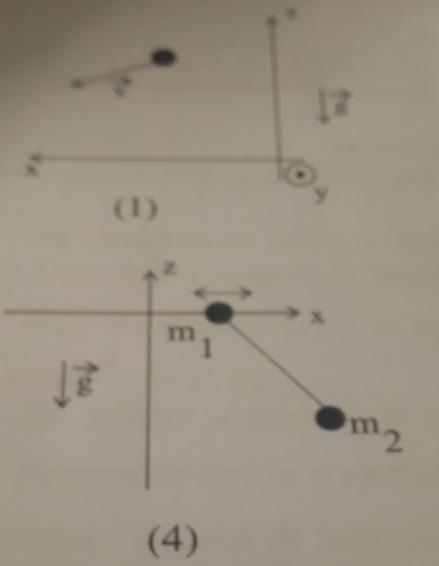
j'ai exercice de mecanique analytique. pendule de masse m2 dont le point de suspension de masse m1 peut se depalcer sans frottement sur un axe horizontal.
voici mon raisonnement T=T1+T2
je voudrais savoir si mon T2 est correct: T2=1/2m2*v^2 avec v= v(x)+v(y)
v(x)=x+lsinƟ et v(y)=-lcosƟ
T2=1/2m2[(dx)^2+l^2(dƟ)^2sin^2Ɵ+l^2sin^2Ɵ+l^2(dƟ)^2cosƟ
avec Ɵ l'angle forme entre m1 et m2 si m1 immobile
merci
Bonsoir
Tu sembles confondre les coordonnées du vecteur position avec les coordonnées du vecteur vitesse...
L'axe vertical est ici l'axe (O,z) selon ton schéma.
Tu sembles confondre dérivée et différentielle. Revois bien ton cours sur la façon d'obtenir les coordonnées du vecteur vitesse connaissant les coordonnées du vecteur position .
T2 est l'énergie cinétique de m2 dans le repère d'étude. T1+T2 est l'énergie cinétique du système constitué des deux masses.
Ensuite il faut exprimer l'énergie potentielle du système en considérant le repère d'étude comme galiléen puis définir le Lagrangien du système : L=T-V , si on note V l'énergie potentielle...
Annuler
connectez vous