Bonjour
1° méthode directe : connaissant les expressions en fonction de t des coordonnées du point mobile dans le repère absolu, on obtient la vitesse absolue (vitesse par rapport au repère absolu) en dérivant par rapport à t les coordonnées du point.
2° : on fait intervenir un repère intermédiaire, dit repère relatif, par rapport auquel les expressions des coordonnées du point sont plus simple. On montre alors que la vitesse absolue est la somme de deux vecteurs :
* la vitesse relative, c'est à dire la vitesse par rapport à ce repère relatif.
* la vitesse d'entraînement.
Cette seconde méthode remplace un calcul direct parfois long par une succession de deux calculs simples.
Tu peux trouver sur le net de nombreux exemples.

Pour la deuxième méthode je dois calculer la vitesse relative et la vitesse d'entraînement , j'imagine que je vais déduire ses expressions d'après l'énoncé ?
pour la première méthode si par exemple j'ai fait une projection sur l'axe oxy comment je peux trouver l'application numérique ? ou bien il suffit de donner l'expression ?

Tout dépend de la façon dont est poser le problème. Poste ici un exemple concret d'exercice que tu ne comprends pas bien si tu veux.

Dans le plan (xoy) un cercle de diamètre OA tourne à vitesse angulaire constante w autour du point O . on lie à son centre ( mobile ) O1 deux axes rectangulaires (O1x1y1) : l'axe O1X1 est dirigé suivant OA . À l'instant initial (t=0). A est sur Ox (Ox et Ox1 sont colinéaires). Un point matériel M . initialement en A . parcourt la circonférence dans le sens positif avec la même vitesse angulaire w .
1- calculer la vitesse absolue par deux méthodes .
2 - calculer l'accélération absolue par deux méthodes . Exprimer les résultats dans la base (i1 j1 ).

Cet exercice est un grand classique. On le trouve ici par exemple (le n°4). Les résultats sont fournis mais sans explications page 3. Essaie par toi-même de trouver les résultats.

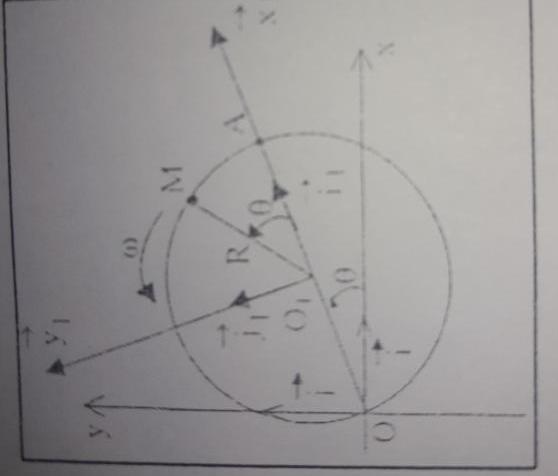
ils ont fait la correction mais j'ai pas compris pourquoi ils ont fait la projection seulement sur l'axe i1j1 ... voilà ce qu'il ont fait :
vecteur OM = OO1 + O1M
OM = Ri1 + Rcosi1 + Rsinj1

Cela est suffisant pour exprimer la vitesse relative. On y ajoute ensuite la vitesse d'entraînement.

ils ont fait ceci pour la méthode de la dérivée du vecteur position .
ce que j'ai compris c que ils ont fait la projection sur l'axe relative pour les deux vecteurs OO1 et O1M et puis ils ont trouvé la relation que j'ai écrit mais pourquoi je ne sais pas.

Pour le calcul direct, exprimer d'abord OM dans la base (i1,j1) présente aussi un intérêt dans la mesure où il est facile ensuite d'exprimer ces deux vecteurs unitaires mobiles en fonction des vecteurs unitaires fixes et .

ils ont obtenu également que la dérivée de 1 par rapport au temps égale la dérivée de × 1 vous pouvez m'expliquer comment je peux trouver la dérivée des vecteurs dans une base mobile et merci

vous pouvez m'aider?

** image supprimée **

Voilà bien un exemple de formule de cours que tu retiens sans l'avoir vraiment comprise...

Pour les deuxième et troisième expressions, il suffit de remplacer i1 par j1 puis par k1avec évidemment :



On peut aussi réfléchir un peu et remarquer qu'ici, puisque la rotation se fait autour de l'axe (O,z) :

  à chaque instant.

Selon la figure, on peut aussi remarquer :



puis dériver par rapport au temps...

merci beaucoup