Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

La projection en électrostatique

Posté par
nazimh 02-02-19 à 20:03

Bonjour,alors voilà pour ce qui de la projection d'un vecteur en électrostatique j'ai jamais compris comment le faire pouvez m'expliquer par exemple dans la solution de cet excercice on a le vecteur Ubd=-cos(o)i-sin(o)j pourquoi comment on a su que cétait ça s'il vous plait
l'énoncé est le suivant:
On place quatre charges ponctuelles aux soûrmets ABCD d'un carré de coté a=lm, et de
centre O, origine d'un repère orthonormé Oxy de vecteurs unitaires i et j (Fig,a)
1. Calculer la résultante des fbrces électrostatique exercée sur la charge (-q) située en D
la figure est un carré avec A en haut a gauche puis B en haut a droite puis C en bas a droite puis D en bas a gauche

Posté par
vanoisere : La projection en électrostatique 03-02-19 à 12:14

Bonjour
Effectivement, tu risque d'avoir des problèmes de compréhension au niveau enseignement supérieur si tu en est là en math !
Voici une fiche, niveau première S, qui va peut-être t'aider :

Ensuite, tu peux scanner puis poster ici un schéma avec les différentes forces qui interviennent dans ton problème puis expliquer ce que tu as été capable de faire.

Posté par
Sayefre : La projection en électrostatique 03-02-19 à 12:23

Bonjour
ce n'est pas complet l'énoncé, ou sont les valeurs des autres charges sur B, C et D.

Posté par
vanoisere : La projection en électrostatique 03-02-19 à 13:52

Bonjour Algerien13
Je crois bien que tu as obtenu réponse à tes questions sur un autre forum...

Posté par
nazimhre : La projection en électrostatique 03-02-19 à 15:10

Non je recherche toujours la réponse pour l'énoncé c'est A=2q B=-q c=-q

Posté par
nazimhre : La projection en électrostatique 03-02-19 à 15:16

c'est là mon probléme comment trouvez ces vecteurs ou plutot comment savoir quand c'est -cos et quand c'est cos et quand c'est sin  pour le i et le j(exemple pour le vecteur Ubd=-coso i -sino j(je sais pourquoi c'est cos et pourquoi c'est sin mais pas pourquoi c'est''-'' j'aurai perso mis coso i + sino j

La projection en électrostatique

Posté par
nazimhre : La projection en électrostatique 03-02-19 à 15:24

vanoise @ 03-02-2019 à 13:52

Bonjour Algerien13
Je crois bien que tu as obtenu réponse à tes questions sur un autre forum...

Merci beaucoup pour ta réponse mais si tu pouvais m'éxpliquer comment savoir quand c'est -cos ou cos ou quand c'est -sin et sin ca serait vraiment sympa

Posté par
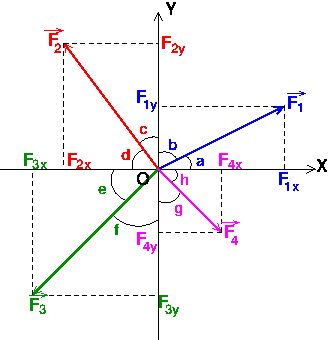
vanoisere : La projection en électrostatique 03-02-19 à 18:56

Voici quatre exemples de vecteurs, un par quadrant. Pour simplifier, les différents angles (a,b,c...) sont tous positifs et compris entre zéro et 90° (\frac{\pi}{2}rad)

Vecteur \overrightarrow{F_{1}} : F_{1x}=\Vert\overrightarrow{F_{1}}\Vert\cdot\cos\left(a\right)=\Vert\overrightarrow{F_{1}}\Vert\cdot\sin\left(b\right)>0\quad;\quad F_{1y}=\Vert\overrightarrow{F_{1}}\Vert\cdot\cos\left(b\right)=\Vert\overrightarrow{F_{1}}\Vert\cdot\sin\left(a\right)>0 \\

Vecteur \overrightarrow{F_{2}} : F_{2x}=-\Vert\overrightarrow{F_{2}}\Vert\cdot\cos\left(d\right)=-\Vert\overrightarrow{F_{2}}\Vert\cdot\sin\left(c\right)<0\quad;\quad F_{2y}=\Vert\overrightarrow{F_{2}}\Vert\cdot\cos\left(c\right)=\Vert\overrightarrow{F_{2}}\Vert\cdot\sin\left(d\right)>0

Vecteur \overrightarrow{F_{3}} : F_{3x}=-\Vert\overrightarrow{F_{3}}\Vert\cdot\cos\left(e\right)=-\Vert\overrightarrow{F_{3}}\Vert\cdot\sin\left(f\right)<0\quad;\quad F_{3y}=-\Vert\overrightarrow{F_{3}}\Vert\cdot\cos\left(f\right)=-\Vert\overrightarrow{F_{3}}\Vert\cdot\sin\left(e\right)<0

Vecteur \overrightarrow{F_{4}} : F_{4x}=\Vert\overrightarrow{F_{4}}\Vert\cdot\cos\left(h\right)=\Vert\overrightarrow{F_{4}}\Vert\cdot\sin\left(g\right)>0\quad;\quad F_{4y}=-\Vert\overrightarrow{F_{4}}\Vert\cdot\cos\left(g\right)=-\Vert\overrightarrow{F_{4}}\Vert\cdot\sin\left(h\right)<0

Il s'agit juste d'une application des formules fournies sur la fiche dont je t'ai fourni précédemment les références. Évidemment, quand la somme de deux angles vaut 90° (angles complémentaires), le sinus de l'un est égal au cosinus de l'autre...

La projection en électrostatique

Posté par
vanoisere : La projection en électrostatique 04-02-19 à 12:53

Je viens de regarder le travail que tu as fait. Il existe une méthode un peu plus rapide qui, en plus, limite le nombre de projections à effectuer. Attention à tes expressions des vecteurs forces. En tenant compte des signes des charges indiqués sur le schéma, les forces exercées par A et C sur D sont attractives, celle exercée par B sur D est répulsive.

\overrightarrow{F_{D}}=k\cdot\dfrac{q_{A}.q_{D}}{DA^{2}}\cdot\overrightarrow{u_{DA}}+k\cdot\dfrac{q_{B}.q_{D}}{BD^{2}}\cdot\overrightarrow{u_{BD}}+k\cdot\dfrac{q_{C}.q_{D}}{CD^{2}}\cdot\overrightarrow{u_{DC}}

L'astuce consiste à remarquer :

\dfrac{\overrightarrow{U_{DA}}}{DA^{2}}=\dfrac{\overrightarrow{DA}}{DA^{3}}=\dfrac{\overrightarrow{DA}}{a^{3}}\quad;\quad\dfrac{\overrightarrow{U_{DC}}}{DC^{2}}=\dfrac{\overrightarrow{DC}}{DC^{3}}=\dfrac{\overrightarrow{DC}}{a^{3}}\quad;\quad\dfrac{\overrightarrow{U_{BD}}}{BD^{3}}=\dfrac{\overrightarrow{BD}}{BD^{3}}=\dfrac{\overrightarrow{BD}}{\left(a\sqrt{2}\right)^{3}}

Ce qui conduit simplement à (je te laisse retrouver les différentes étapes du calcul) :

\overrightarrow{F_{D}}=k\cdot\dfrac{q^{2}}{a^{3}}\cdot\left(\overrightarrow{DA}+\overrightarrow{DC}+\dfrac{\overrightarrow{BD}}{2\sqrt{2}}\right)

En développant en passant par le point O :

\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DO}+\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{OC}=2\overrightarrow{DO}

\dfrac{\overrightarrow{BD}}{2\sqrt{2}}=-\dfrac{\overrightarrow{DO}}{\sqrt{2}}

Je te laisse terminer les calculs. On voit bien que la résultante des vecteurs forces à la direction et le sens du vecteur \overrightarrow{DO}, le seul que tu vas devoir exprimer en fonction de et .
Attention : j'ai tenu compte des charges indiquées sur ton schéma, pas de celles dont tu parles dans ton message du   03-02-19 à 15:10...

Posté par
vanoisere : La projection en électrostatique 04-02-19 à 16:57

Petit oubli dans la première formule explicitant le vecteur force FD. J'ai orienté les vecteurs unitaires dans les sens des vecteurs forces de sorte qu'il faut considérer dans les formules les valeurs absolues des charges. J'ai oublié les traits verticaux... Pas de problème pour la suite a priori !

Posté par
nazimhre : La projection en électrostatique 04-02-19 à 19:22

vanoise @ 03-02-2019 à 18:56

Voici quatre exemples de vecteurs, un par quadrant. Pour simplifier, les différents angles (a,b,c...) sont tous positifs et compris entre zéro et 90° (\frac{\pi}{2}rad)

Vecteur \overrightarrow{F_{1}} : F_{1x}=\Vert\overrightarrow{F_{1}}\Vert\cdot\cos\left(a\right)=\Vert\overrightarrow{F_{1}}\Vert\cdot\sin\left(b\right)>0\quad;\quad F_{1y}=\Vert\overrightarrow{F_{1}}\Vert\cdot\cos\left(b\right)=\Vert\overrightarrow{F_{1}}\Vert\cdot\sin\left(a\right)>0 \\
C'est ce dont j'avais besoin ,merci à toi maintenant j'ai plus de probléme j'ai bien compris

Vecteur \overrightarrow{F_{2}} : F_{2x}=-\Vert\overrightarrow{F_{2}}\Vert\cdot\cos\left(d\right)=-\Vert\overrightarrow{F_{2}}\Vert\cdot\sin\left(c\right)<0\quad;\quad F_{2y}=\Vert\overrightarrow{F_{2}}\Vert\cdot\cos\left(c\right)=\Vert\overrightarrow{F_{2}}\Vert\cdot\sin\left(d\right)>0

Vecteur \overrightarrow{F_{3}} : F_{3x}=-\Vert\overrightarrow{F_{3}}\Vert\cdot\cos\left(e\right)=-\Vert\overrightarrow{F_{3}}\Vert\cdot\sin\left(f\right)<0\quad;\quad F_{3y}=-\Vert\overrightarrow{F_{3}}\Vert\cdot\cos\left(f\right)=-\Vert\overrightarrow{F_{3}}\Vert\cdot\sin\left(e\right)<0

Vecteur \overrightarrow{F_{4}} : F_{4x}=\Vert\overrightarrow{F_{4}}\Vert\cdot\cos\left(h\right)=\Vert\overrightarrow{F_{4}}\Vert\cdot\sin\left(g\right)>0\quad;\quad F_{4y}=-\Vert\overrightarrow{F_{4}}\Vert\cdot\cos\left(g\right)=-\Vert\overrightarrow{F_{4}}\Vert\cdot\sin\left(h\right)<0

Il s'agit juste d'une application des formules fournies sur la fiche dont je t'ai fourni précédemment les références. Évidemment, quand la somme de deux angles vaut 90° (angles complémentaires), le sinus de l'un est égal au cosinus de l'autre...

La projection en électrostatique

Posté par
nazimhre : La projection en électrostatique 04-02-19 à 19:23

C'est ce dont j'avais besoin ,merci à toi maintenant j'ai plus de probléme j'ai bien compris


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !