Niveau école ingénieur

La pression totale de l’eau sur une vanne

Posté par
nano21 18-08-17 à 18:33

Bonsoir tout le monde,
Encore j'aurai besoin de votre aide ....et je vous remercie infiniment pour votre  collaboration.

voici l'énoncé:
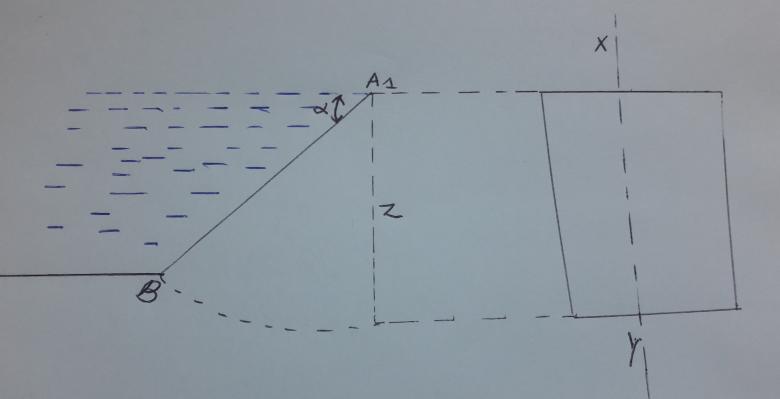
Une vanne trapézoïdale de grande base B , de petite base b et de hauteur h est inclinée sur l'horizontale d'un angle α.
Exprimer en fonction de B, b, h, α :
La pression totale de l'eau sur la vanne ;
La profondeur du centre de pression.
Application : B= 3,00m ; b= 2,00 m ;  h= 4,50 m ; g= 9,81 m/s² ; α = 30°

SOLUTION

En prenant
 Un axe vertical Az dirigé vers le bas
 Un axe Ax suivant AB,

On décompose la vanne en un élément :
 De longueur l
 De largeur dx, correspondant à dz.

La force résultante sur cette surface est :

dF= ρ. g.l.z.dx

Donc Il faut trouver
 z en fonction de x,
 l en fonction de x. :     l(x) =  B+ ((b-B)/h) (x)    =   3+(2-3)/4,5)(x)

La force est le volume de la pression sur la surface.

• La surface centrale rectangulaire, c'est un prisme rectangle dont la hauteur est la pression, formule Bh/2 (B pour base) .

F1 = [hauteur]  x  [surface]/2 =[ρ .g.h.sin(a)].[h.b]/2

= ρ .g.sin(a)h²b/2

• Les surfaces triangulaires, tétraèdre, formule Bh/3

F2 =[ρ.g.h.sin(a)].[h.(B-b)/2/2}]/3 = ρ.g.sin(a).h²(B-b)/6

Donc :
F =  F1+F2 =( ρ.g.sin(a) x (b.h²/2 )   +   h².(B-b)/6) = 99329 Pa

La pression totale de l'eau sur la vanne est donc : 99329 Pa

La profondeur du centre de pression :

Pour le centre de poussée il faut écrire que le moment de la force résultante par rapport à A est égal à la somme des moments élémentaires dM=dF.x

Nous avons :
• Le centre de pression est sur l'axe xy ,
On recherche alors l'éloignement par rapport au point A moment d'inertie trapèze

(b+B) h x 3/12  et (b+B)*h/2 * h/2 =   (b+B)h²/4

d'où éloignement par rapport à A = moment d'inertie/dernier calcul  =  h/3

Donc
Le centre de poussé éloigné de 4,5/3=1,5 mais avec un plan incliné d'où z = 1,5 sin30° =0,75m

La pression totale de l’eau sur une vanne

Posté par re : La pression totale de l’eau sur une vanne 18-08-17 à 21:53

Bonsoir
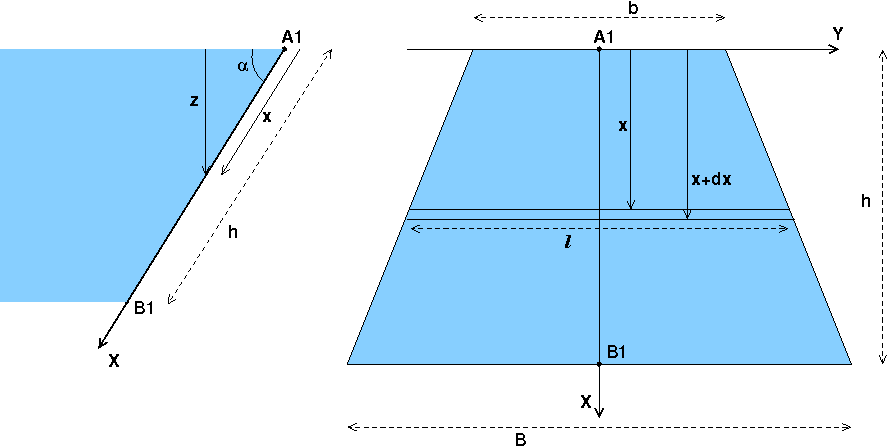
Je crois que tu commences bien sur le modèle de l'exercice que tu as fait précédemment mais tu changes brutalement de méthode en cours de route en décomposant la surface en trois, pourquoi ? Je reprends sans modification tes notations et le début de ton raisonnement qui me semble correct mais ton schéma ne me parait pas très clair....
Si la grande base du trapèze est bien, comme semble l'indiquer ton schéma, la plus profonde, l'expression de la largeur de la bande élémentaire d'abscisse x est :
$l=b+\frac{B-b}{h}\cdot x$ , x=0 correspondant à la petite base du trapèze et à la surface libre de l'eau.
De plus : z=x.sin()
Cela conduit à une force élémentaire de poussée :

$dF=\rho.g.l.z.dx=\rho.g.\sin\left(\alpha\right).\left(b+\frac{B-b}{h}\cdot x\right).x.dx$
Il te reste à intégrer de x = 0 à x=h...
Inutile de décomposer la surface en trois ! un simple calcul intégral suffit !
Je te laisse réfléchir à cela et revoir ton calcul...

Posté par re : La pression totale de l’eau sur une vanne 18-08-17 à 22:51

Voici deux schémas explicitant comment j'ai compris l'énoncé mais celui-ci ,tel que tu l'as reproduit, n'est pas précis : il faut peut-être permuter B et b.
Celui de gauche reprends le tien avec quelques compléments ; celui de droite est une vue de face de la plaque en forme de trapèze.

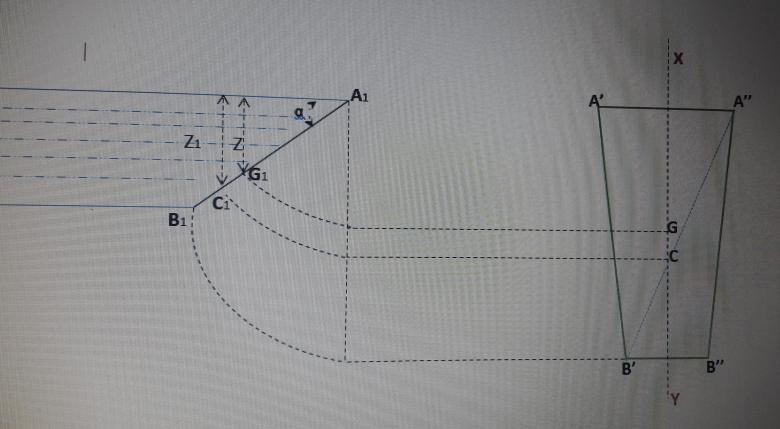
La pression totale de l’eau sur une vanne

Posté par re : La pression totale de l’eau sur une vanne 03-09-17 à 15:19

Bonjour Vanoise!!J'ai mis un peu de temps à te répondre..désolée..

Je pense vanoise qu'il est possible de résoudre l'exercice sans passer par le calcul intégral.
Avec le schéma ci-joint, voilà ce que je propose :
- exprimer XG en fonction de h,B et b puis la surface de la vanne en fonction de B,b et h et enfin z en fonction de XG et alpha. nous enduirons P.

La poussée totale de l'eau sur la vanne est donnée par la formule générale :
P : ϖ Z ɯ
Avec :
ϖ poids volumique de l'eau
Z profondeur du centre de gravité
ɯ surface de la vanne

Qu'est ce que t'en penses?

La pression totale de l’eau sur une vanne

Posté par re : La pression totale de l’eau sur une vanne 03-09-17 à 16:25

Bonjour

Citation :
Qu'est ce que t'en penses?

Aïe ! Tu sembles revenue au niveau que tu affichais dans ton tout premier message sur ce forum alors que tes derniers messages étaient assez encourageants !Ce que tu viens d'écrire est faux a priori. Evidemment, on peut imaginer des situations particulières où certaines influences en compensant d'autres, il est possible d'obtenir ce résultat mais il ne faut absolument pas considérer ce que tu as écrit comme correct dans le cas général :
ton raisonnement serait valide pour une pression identique en tout point de la surface, ce qui n'est pas le cas : la pression augmente avec la profondeur !
Tu as déjà expliqué que tu reprends tes études : le calcul intégral à faire ici , que je t'ai présenté précédemment, ne dépasse pas le niveau d'une terminale ES (pas S !). Il va être difficile d'obtenir un niveau ingénieur sans faire le moindre calcul intégral. Les formulaires ne font pas tout !
Il te faut reprendre les explications de mes messages précédents. En revanche, le schéma que tu viens de poster montre que la plus grande longueur du trapèze est en x=0 et non en x = h. Il y a donc lieu, par rapport à mon message du 18-08-17 à 21:53 de permuter B et b.
Le résultat obtenu pour la poussée ne correspond pas à ce que tu as proposé dans ton premier message. Erreur également concernant la position du centre de poussée. Tu la trouves ne dépendant que de h : diminuer b par rapport à B, conduit à un centre de poussée moins profond. La position du centre de poussée doit donc dépendre de h mais aussi du rapport (B/b).
Bon courage ! Je te laisse réfléchir à tout cela et proposer une nouvelle solution.

Posté par re : La pression totale de l’eau sur une vanne 03-09-17 à 20:59

Comme déjà expliqué dans le topic sur la plaque en forme de demi disque, le calcul intégral qui intervient dans l'expression de la force de poussée est analogue à celui permettant d'obtenir l'abscisse du centre de gravité. De là j'imagine, la tentation d'avoir recours à un formulaire. Mais ici, franchement: il suffit de connaître les expressions des primitives de x et de son carré...

Posté par re : La pression totale de l’eau sur une vanne 04-09-17 à 14:41

Bonjour
Pour illustrer mes propos précédents, je te fournis l'expression de la force de poussée par les deux méthodes. Je reprends le contenu de mon message du 18-08 en permutant b et B pour tenir compte de ton dernier schéma. La largeur de la bande élémentaire d'abscisse x est :

$l=B-\frac{B-b}{h}\cdot x$
La force élémentaire de pression exercée sur la bande élémentaire est ainsi :

$dF=\rho.g.l.z.dx=\rho.g.\sin\left(\alpha\right).\left(B-\frac{B-b}{h}\cdot x\right).x.dx$

Première méthode : on intègre cette expression entre x = 0 et x = h. C'est hyper simple : il suffit de connaître les expressions des primitives de x et de son carré :

$F=\rho.g.\sin\left(\alpha\right).\int_{0}^{h}\left(B-\frac{B-b}{h}\cdot x\right).x.dx$

$\int_{0}^{h}\left(B-\frac{B-b}{h}\cdot x\right).x.dx=\left[B.\frac{x^{2}}{2}-\frac{B-b}{h}\cdot\frac{x^{3}}{3}\right]_{0}^{h}=B.\frac{h^{2}}{2}-\frac{B-b}{h}\cdot\frac{h^{3}}{3}=\frac{h^{2}}{6}\cdot\left(B+2b\right)$

$F=\frac{1}{6}\cdot\rho\cdot g\cdot\sin\left(\alpha\right)\cdot h^{2}\cdot\left(B+2b\right)$

L'application numérique, arrondie à trois chiffres significatifs, conduit à :

$F=1,16.10^{5}N$

Deuxième méthode : on remarque que le calcul intégral est analogue à celui utilisé pour déterminer l'abscisse du centre de gravité G d'une plaque homogène ayant la forme et les dimensions de cette vanne. Cela conduit à :

$\int_{0}^{h}\left(B-\frac{B-b}{h}\cdot x\right).x.dx=S.x_{G}$

S est l'aire de la surface du trapèze. Il s'agit effectivement d'une formule classique :

$S=h\cdot\frac{B+b}{2}$

En revanche, l'expression de l'abscisse du centre de gravité d'un trapèze isocèle n'est pas vraiment un classique et donc, à moins évidemment d'avoir un « bon » formulaire, sa démonstration est plus longue que le calcul intégral direct de la première méthode. On obtient :

$x_{G}=\frac{h}{3}\cdot\frac{B+2b}{B+b}$

Je te laisse vérifier que cette seconde méthode conduit bien au même résultat final.