Niveau école ingénieur

la pression dans une coche

Posté par
nano21 16-08-17 à 12:03

Bonjour à toutes et tous, j'aurais besoin encore de votre aide pour cet exercice svp,si vous pourriez me corriger. je vous remercie.

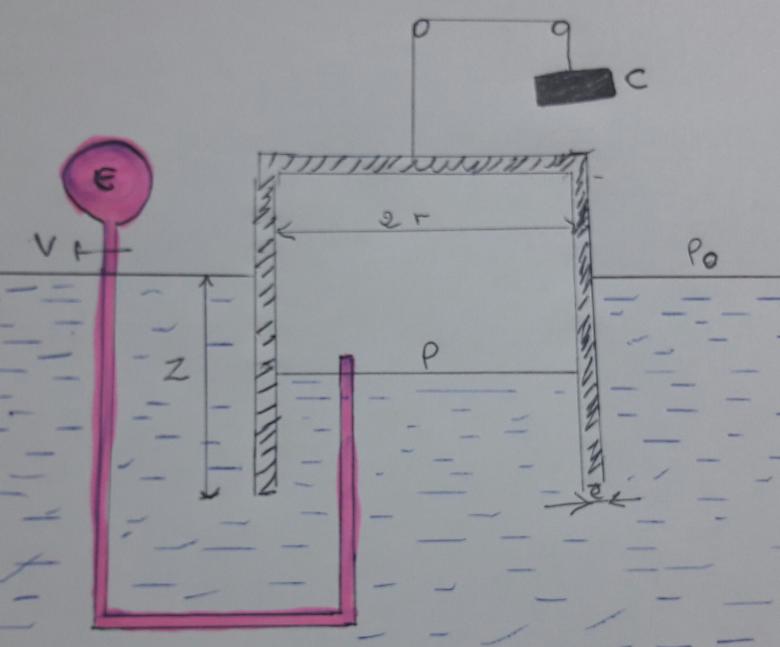
Soit une cloche cylindrique ouverte à une extrémité, placée verticalement dans l'eau, l'extrémité ouverte se trouvant à la partie inférieure, cette cloche, munie d'un contrepoids C, a pour rayon intérieur  r=200 mm, et pour épaisseur  e=2mm.

L'intérieur de la cloche peut être mis en communication, au moyen d'une tuyauterie munie d'une vanne V, avec une enceinte E contenant un gaz sous pression. Lorsque la pression p, évaluée en mm d'eau, règne à l'intérieur de la cloche, celle-ci s'enfonce dans l'eau de z=15mm.
Quel sera cet enfoncement si après ouverture de la vanne V, la pression dans la coche devient p+0,2mm ?

2 r= 400 mm
Z  = 15 mm
e= 2mm

Solution
Quel sera cet enfoncement si après ouverture de la vanne V, la pression dans la coche devient p + 0,2mm ?

Les éléments à prendre en compte :
 La force de pression qu'exerce l'eau sur la paroi intérieure immergée ;
 Poussée d'Archimède ;
 La force de pression qu'exercice le gaz P sur la paroi intérieure ;
 La pression atmosphérique exercée sur la cloche.

Donc :

d'une part on considère  la variation de force (due à l'ouverture de la vanne) due à la variation de pression (0,2mm eau) fois la surface intérieure (section) du cylindre   r2 :

Δ F =Δp   *  r2
Et, d'autre part, la variation de la force d'Archimède due à l'ouverture de la vanne :

  ΔF = ΔV  *  ρ eau *9,81

Avec  Δ V = 2 *r*e * Δ z

et

   Δ z = r/(e*2*9,81*1000) *   Δp

  Δz = 5*10^-3 *   Δp

Et, pour un   Δp de 2Pa (0,2mm d'eau) cela donne :

  Δz = 5*10^-3 *   Δp
  Δz = 1cm

1cm de déplacement pour une variation de pression de 0,2mm.

la pression dans une coche

Posté par re : la pression dans une coche 16-08-17 à 17:00

Bonjour
Je pense que tu as compris l'essentiel mais il y a quelques améliorations possibles...
Tu parles de déplacement de la cloche sans préciser s'il s'agit d'un déplacement vers le haut ou vers le bas. Attention aussi à ne pas mélanger dans une même formule valeurs littérales et valeurs numériques. Cela te fait perdre tout contrôle sur l'homogénéité des formules alors que justement, la vérification de cette homogénéité est un moyen efficace pour éviter de grosses erreurs...
Entre l'état initial d'équilibre et l'état final d'équilibre, seules les intensités de deux forces verticales varient ; la somme algébrique des variations de ces deux intensités de force est donc nulle. Ces deux forces sont :
1° la poussée d'Archimède d'intensité initiale :
F_A=2.r.e._eau.g.z
Sa variation est donc : F_A=2.r.e._eau.g.z
2° la force pressante exercée par le gaz, d'intensité initiale :
F_g=P..r²
Sa variation est donc :
F_g=P..r²
La somme des deux variations est nulle :
2.r.e._eau.g.z+P..r²=0
D'où :

$\Delta z=-\frac{\Delta P}{\rho_{eau}\cdot g}\cdot\frac{r}{2e}$

L'énoncé précise que la variation de pression est équivalente à une hauteur d'eau de 0,2mm :

$\frac{\Delta P}{\rho_{eau}\cdot g}=0,2mm$

D'où :

$\Delta z=-\frac{0,2\cdot200}{4}=-10mm$

La valeur de z diminue puisque z<0. La cloche se soulève donc, par rapport à la surface libre de l'eau de 10mm.
En terme de difficulté : rien à voir avec l'exercice précédent !