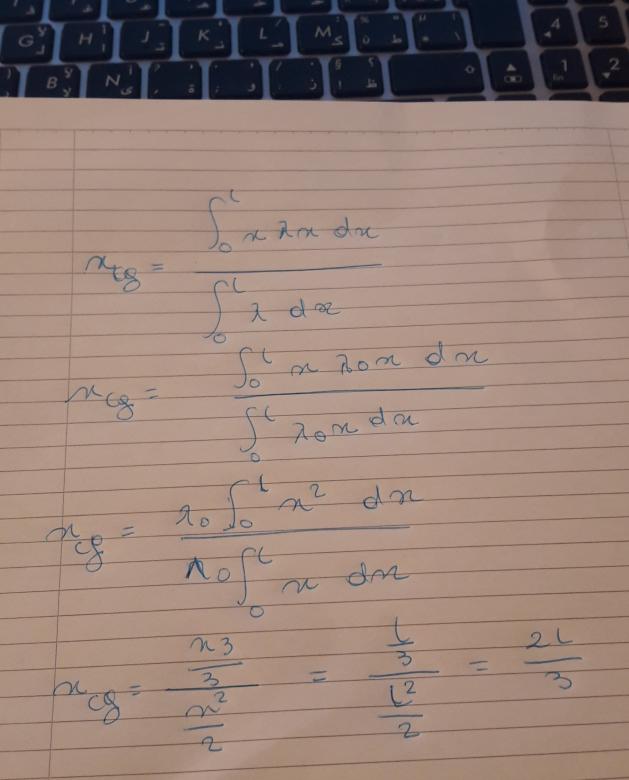Niveau école ingénieur

la position du centre de gravité d'une barre

Posté par
nano21 07-07-17 à 22:05

Bonsoir tout le monde ,
voici un exercice que j'ai résolu  mais je ne suis pas sûr de ma réponse, donc si vous pouvez  vérifier s'il vous plait....je vous remercie .

On considère une barre AB de longueur  l   et de section constante   s, dont la masse volumique   ρ   varie de façon linéaire entre le point A(ρA) et le point B(ρB)
Déterminer la position du centre de gravité de la barre AB

La masse volumique ρ varie de façon linéaire entre le point A  et  B
Nous considérons un élément infiniment petit de longueur dx et de section s pour lequel on admettra que la masse volumique est constante.
La densité linéaire (masse / longueur) de la barre varie avec la distance x de l'origine comme
dm = ρ dx = (A + Bx) dx
La masse linéique λ(x) au point x : dm = λ(x)dx.

λ = λ0x
xcg =(∫_0^l▒〖xλx  dx〗)/(∫_0^l▒〖λ  dx〗)

xcg =(∫_0^l▒〖xλo x  dx〗)/(∫_0^l▒〖λox  dx〗)

xcg =(λo∫_0^l▒〖x²  dx〗)/(λo∫_0^l▒〖x  dx〗)
xcg =  ((x3  )/3)/ (x^2/2) =  ((l  )/3)/ (l^2/2)=  2l/3

Posté par re : la position du centre de gravité d'une barre 07-07-17 à 22:23

Bonsoir
difficile de juger ton travail : tes formules sont illisibles...
Tu sembles démarrer par la bonne méthode mais impossible de juger la suite...

Posté par re : la position du centre de gravité d'une barre 07-07-17 à 22:35

bonsoir vanoise ..oui c'est vrai on ne voit pas bien le signe de l'intégral ..... ok je vais écrire la solution sur papier et je te l'envoie ..merci vanoise

Posté par re : la position du centre de gravité d'une barre 07-07-17 à 22:48

OK
N'oublie pas de réfléchir au réalisme de ton résultat : le fait de trouver la position de G indépendante de _(A) et de _(B) n'est pas réaliste :
1° le cas particulier : _(A) = _(B) correspond à une tige homogène et donc à AG=x_cg=l/2  ;
2° le cas _(A) > _(B)  correspond à une moitié "gauche" plus lourde que la partie "droite" donc à AG=x_cg<l/2 ;
3° le cas _(A) < _(B)  correspond à une moitié "gauche" plus légère que la partie "droite" donc à AG=x_cg>l/2 ...

Posté par re : la position du centre de gravité d'une barre 07-07-17 à 22:52

J'espère que c'est lisible

$la position du centre de gravité d\'une barre$

Posté par re : la position du centre de gravité d'une barre 07-07-17 à 22:57

Le faite que la masse volumique ρ varie de façon linéaire entre le point A et B se traduit par une relation ρ= λ(x)+μ ??

Posté par re : la position du centre de gravité d'une barre 07-07-17 à 23:33

Ton problème provient d'une mauvaise expression de la masse volumique donc aussi de la masse linéique.
La masse volumique varie de façon affine (pas linéaire selon les professeurs de mathématiques) en fonction de la distance x au point A. Cela donne :

$\rho(x)=\rho_{A}+\frac{\rho_{B}-\rho_{A}}{l}\cdot x$
La masse dm de la tranche élémentaire comprise entre les sections droites d'abscisses x et (x+dx) vaut :
$\\ dm=s.\rho\left(x\right).dx$

Tu peux poser éventuellement : $\lambda\left(x\right)=s.\rho\left(x\right)$ ...
La masse m de la tige est ainsi :

$m=\intop_{0}^{l}s.\rho\left(x\right).dx=s.\left[\rho_{A}.l+\intop_{0}^{l}\frac{\rho_{B}-\rho_{A}}{l}\cdot x.dx\right]=s.l\cdot\frac{\rho_{B}+\rho_{A}}{2}$
Résultat réaliste et même intuitif : la masse est celle qu'aurait une tige homogène dont la masse volumique serait la masse volumique moyenne.

$AG=x_{cg}=\frac{\intop_{0}^{l}x.dm}{m}$

$\intop_{0}^{l}x.dm=\intop_{0}^{l}s.\rho\left(x\right).x.dx=s.\left[\int_{0}^{l}\rho_{A}.x.dx+\intop_{0}^{l}\frac{\rho_{B}-\rho_{A}}{l}\cdot x^{2}.dx\right]=s.\rho_{A}.\frac{l^{2}}{2}+s.\frac{\rho_{B}-\rho_{A}}{l}\cdot\frac{l^{3}}{3}$

$\intop_{0}^{l}x.dm=s.l^{2}.\left(\frac{\rho_{B}}{3}+\frac{\rho_{A}}{6}\right)$
Au final :

$\boxed{AG=x_{cg}=l\cdot\frac{2\rho_{B}+\rho_{A}}{3\left(\rho_{A}+\rho_{B}\right)}}$

Remarque : on peut aussi écrire :

$\frac{x_{cg}}{l}=\frac{2\frac{\rho_{B}}{\rho_{A}}+1}{3\frac{\rho_{B}}{\rho_{A}}+3}$

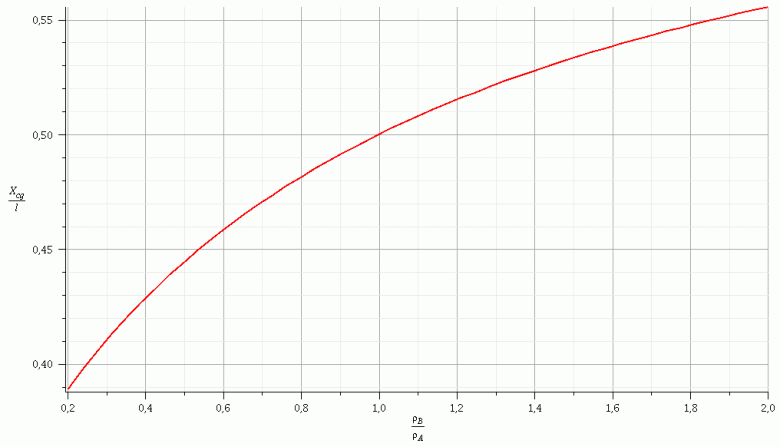
Je représente ci-dessous la courbe représentant les variations de $\frac{x_{cg}}{l}$ en fonction de $\frac{\rho_{B}}{\rho_{A}}$ . On peut facilement vérifier que cette courbe est en accord avec mon message précédent sur le réalisme du résultat.

$la position du centre de gravité d\'une barre$