Inscription / Connexion Nouveau Sujet
La flexion déviée
Salut.
On a commencé le cours de Résistance des Matériaux le chapitre de Flexion simple . j'ai quelques questions concernant à ça:
J'ai un problème dans le calcule de déplacement :
J'ai l'exemple suivante :
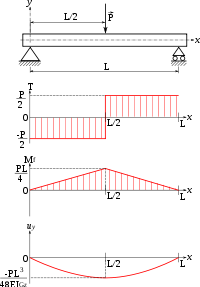
Une poutre appuyé sur deux appuis ( appuie simple et l'autre double) avec une charge . voilà le figure
Et je trace le diagrammes des Mf +Effort tranchant : D'après le diagramme on trouve qu'il y a deux équation de Mf ( 1 avant la charge .2 après la charge ) cela qui me pose le problème : dans l'exercice il sont demander de calculer le déplacement j'ai l'équation suivant :
y''=- (Mf/I×E)
tel que
I: moment d'inertie
E: module de young
Mon problème :
Mais dans notre exemple il y a deux équation de Mf (avant et après la charge) . je ne sais pas quelle est l'équation je peut utiliser ?
Merci.
Bonjour,
Tu dois déterminer le déplacement de ta poutre sur les deux tronçons.
En utilisant les conditions aux limites, tu en déduis que le déplacement (dans ton exemple) est maximal et qu'il y a une continuité de la fonction déplacement en ce point.

Merci Monsieur pour votre réponse . j'ai déjà fait ça ( le calcul de T et Mf et j'ai tracé aussi les diagrammes ) . J'ai un problème dans le calcul de déplacement.
*** message déplacé ***
Pourrais-tu écrire les équations du déplacement pour chaque tronçon et effectuer la double intégration stp ?
Pour déterminer les constances d'intégrations, tu peux t'aider des conditions aux limites (à l'appui par exemple).

*** message déplacé ***
Of caurse Sir,
J'ai commencé par les réactions d'appuis :
Ray+Rby=0
Ray=P/2 ; Rby=P/2
Pour le moment fléchissant : quand
Et pour
Je trouve :
Pour le déplacement  :
:
Si je travaille par trançon ça veut
Je trouve
Les condition initial :
x=0 j'ai y=0 donc C2=0
Mais pour
x=l/2 je ne connais pas la valeur de y=??
J'attends votre réponse
*** message déplacé ***
Ra = Rb = P/2 --> OK
Diagramme des effort intérieurs :
Effort tranchant Ty :
x compris entre L/2 et L : Ty = +P/2
x compris entre 0 et L/2 : Ty = +P/2 - P = -P/2
Moment fléchissant Mfz :
x compris entre L/2 et L : Mfz = +P/2*(L-x)
x compris entre 0 et L/2 :
Mfz = +P/2*(L-x) - P*(L/2 - x)
Mfz = P/2*x
Equation du déplacement :
Soit y1 le déplacement entre x = 0 et x = L/2
y2 le déplacement entre x = L/2 et x = L
Il faut que tu aboutisses aux deux équations de déplacement avec les 4 constantes d'intégration (deux par tronçons).
Tu as 4 conditions aux limites :
- condition (1) : x = 0 => y1(0) = 0
- condition (2) : x = L => y2(L) = 0
La fonction déplacement est continue en x = L/2 on peut donc écrire :
- condition (3) : y1(L/2) = y2(L/2)
Etant donné qu'on sait que le déplacement atteint un extrémum en x = L/2, on peut également écrire que
- condition (4) : dy1(L/2)/dx = dy2(L/2)/dx
soit un système de 2 équations, 2 inconnus à résoudre pour déterminer les 2 dernières constantes d'intégration.
*** message déplacé ***
Coool . merci monsieur . et la même chose pour la contrainte (par trançon) thanx your help.
*** message déplacé ***