Bosoir pileus,

tu as raison de protester, car ce n'est pas une expression couramment utilisee. En mathematiques, une fonction y = f(x) est stationnaire si en une valeur x₀ de x, la derivee premiere y' est nulle. La fonction presente donc en x₀ un extremum, minimum ou maximum, c'est a dire qu'au voisinage de x₀ et est localement constante.
Elle est hyperstationnaire si, en x₀, non seulement la derivee premiere y' et nulle, mais aussi les derivees d'ordre superieur, y'', y''' etc...

Dans le cas des bobines d'Helmoltz, le champ magnetique B1 sur l'axe est donne par la relation que tu peux retrouver sur le site . Comme B1(x) et une fonction paire, B1 et extremum pour x = 0 (c'est un maximum). la premiere derivee non nulle est donc d²B1/dx², qui depend du rayon R des bobines et de la distance D qui separe leurs centres. Si on ajuste R et D pour que le coefficient qui multiplie la derivee seconde soit nul lui aussi,alors B1 ne depend de x que par un terme en x⁴, donc reste constant sur un plus grand domaine de variations de x au voisinage de x = 0.
Le petit schema ci-dessous t'aidera a comprendre mon explication.

Prbebo.

erratum : sur la figure jointe ci-dessus, il faut lire "est nulle" au lieu de "et", et d²y/dt² au lieu de d²y/dt₂. Je ferais mieux d'aller me coucher, moi...

merci beaucoup pour cette trésor que tu m'a donné
j'ai trouvé l'expression du champs magnétique B =B_0 (1/((l-x)^2+R^2 )^(3/2) +1/((l+x)^2+R^2 )^(3/2) ) avec 2l la distance qui sépare les deux bobines et R le rayons commun de cette bobine B_0 est une constante
alors pour montrer l'égalité il suffit de chercher l en fonction de R en effectuant le développement limité
(càd B=B(l)+x(dB(x)/dx)x=l+(x^2/2)(d^2B/dx)x=l+....
on met (d^2B/dx)(x=l)=0
c'est ça??

Bonjour Pileus,

ton message est a la limite de la comprehension... je suppose que tu veux savoir comment on trouve la distance qui separe les centres des bobines pour avoir un champ magnetique pratiquement constant sur leur axe. OK ? Je vais de donner les etapes du calcul, mais sans trop detailler les calculs intermediaires (sinon j'en ai jusqu'a ce soir) :

Champ cree par une bobine de centre C, en un point P situe a la distance CP = z sur son axe :
La relation de Lagrange-Helmholtz donne facilement B = ₀NIR²/2.(R² + z²)^-3/2.

Champ cree en P par deux bobinnes:
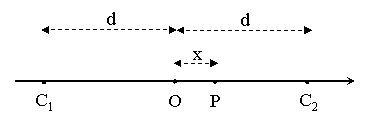
Cf la figure ci-dessous pour les notations : on fait d'abord un changement d'origine en placant le point O au milieu du segment C₁C₂, on pose O = x. La distance qui separe les deux centres C₁ et C₂ et C₁C₂ = 2d (je prefere la lettre d a l, qui passe tres mal sur le forum). On a donc C₁P = d + x, et C₂P = d - x.
Le champ magnetique en P s'ecrit B(x) = K.(A₁^-3/2 + A₂^-3/2), avec K = ₀NIR²/2, A₁ = R² + (d + x)², A₂ = R² + (d - x)². On va avoir besoin des derivees de A₁ et de A₂ par rapport a x, soit A₁/x = 2(d + x) et A₂/x = 2(d - x)

Ensuite, on va en effet faire un developpement limite de B(x) en fonction de x. On ecrit donc B(x) = B(x=0) + (x²/2).²B/x²_(x=0) + 0(x⁴). Pourquoi n'y a-t-il pasde termes en x et en x³ ? simplement parce que B(x) est une fonction paire de x.
Pour obtenir ²B/x², il faut malheureusement commencer par B/x... Donc :
B/x = 3K.[-(d + x).A₁^-5/2 + (d - x).A₂-^5/2].
On rederive (attention aux signes - qui arrivent... et on obtient
²B/x² = 3K.[-A₁^-5/2 + 5.(d + x)².A₁^-7/2 - A₂^-5/2 + 5.(d - x)².A₂^-7/2].
Lorsque x = 0, on a A₁ = A₂ = R² + d². La derivee seconde de B(x) pour x = 0 s'ecrit donc, apres avoir rassemble convenablement les termes :
²B/x²_{(x = 0)} = 3₀NIR².(R² + d²)^-7/2.[4d² - R²].

Ouf ! On voit que cette derivee est nulle si le crochet est nul, soit pour une distance d egale a R/2. Le champ magnetique sur l'axe des deux bobines est donc constant au 4^ieme ordre pres en x si la distance C₁C₂ entre les centres est egale au rayon R.
La norme de B vaut alors 2K.A₁(0), soit tous calculs faits B = ₀NI/R.(5/4)^-3/2.  Ca ne s'invente pas...

Si tu as des questions sur le detail de  ce calcul, tu peux les poser, mais sois clair stp, car tes mels sont tres difficiles a lire.

Prbebo.