Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... IutForum Supérieur (IUT) PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau iut
Partager :

Joint de Cardan

Posté par
lidlkidjoe 16-01-21 à 09:10

Bonjour, j'ai quelques soucis pour exprimer la loi des vitesses entrée/sortie dans le repère du croisillon.

La question qui nous est posée est :
Ecrire la relation qui existe entre \Omega et les angles d'Euler, en déduire le rapport de \LARGE\dfrac{\Omega}{\dot{\Psi}}


Je propose :

On notera que \Omega = \Omega \overrightarrow{x}\vspace*{0.2cm}\\

\overrightarrow{\Omega}(S/R_1) = \dot{\theta}\overrightarrow{u} + \dot{\Psi}sin\theta\overrightarrow{w} +(\dot{\phi} + \dot{\Psi}cos\theta)\overrightarrow{z} \vspace*{0.3cm} \\ \Omega(cos\phi\overrightarrow{u} + sin\phi\overrightarrow{w}) = \dot{\Theta}\overrightarrow{u} + \dot{\Psi}sin\theta\overrightarrow{w} + (\dot{\phi} + \dot{\Psi}cos\theta)\overrightarrow{z} \\

On projette sur le vecteurs tous unitaires.

\Omega(cos\phi + sin\phi) - \dot{\theta} - \dot{\phi} = \dot{\Psi}(sin\theta + cos\theta) \vspace*{0.2cm} \\  \Omega(cos\Phi + sin\Phi) = \dot{\Psi}(sin\theta + cos\theta) \vspace*{0.2cm} \\ \dfrac{\Omega}{\dot{\Psi}} = \dfrac{sin\theta+cos\theta}{cos\phi + sin\phi}

Je joints un schéma et les figures planes. Pourriez-vous, s'il-vous-plaît, m'aider dans la démarche car j'ai l'impression de ne pas bien saisir ce qu'on me demande et par conséquent de ne pas répondre correctement.
Merci d'avance pour toute aide.

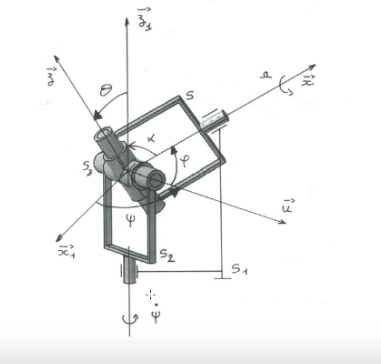
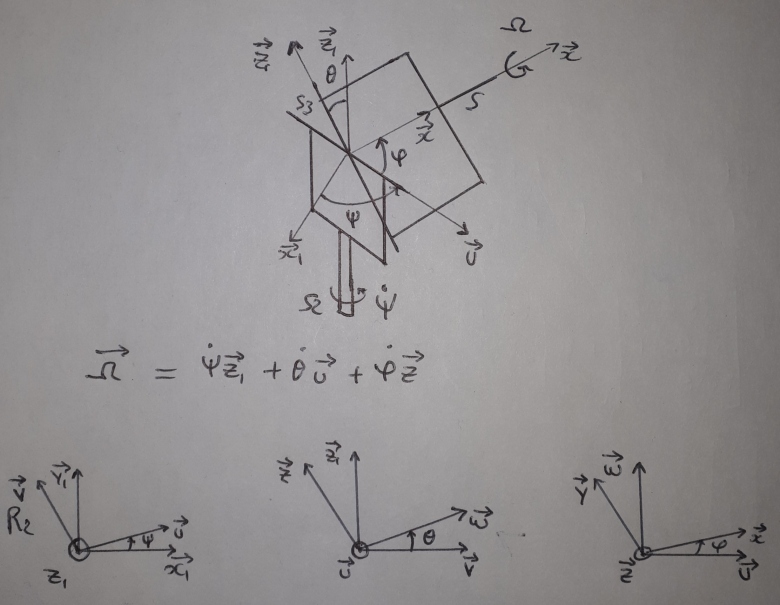
Joint de Cardan

Joint de Cardan

Posté par
vanoisere : Joint de Cardan 16-01-21 à 11:25

Bonjour
OK pour les deux premières lignes. Ensuite il faut identifier les composantes de gauche et de droite suivant les trois vecteurs unitaires. Ce n'est pas du tout ce que tu as fait. On obtient quelque chose de beaucoup plus simple.

Posté par
lidlkidjoere : Joint de Cardan 16-01-21 à 13:12

Bonjour @vanoise, je ne comprends pas ce que tu entends par identifier les vecteurs unitaires. Il faudrait que je regroupe les composantes de même vecteur ?

Posté par
vanoisere : Joint de Cardan 16-01-21 à 13:44

\left(\overrightarrow{u},\overrightarrow{w},\overrightarrow{z}\right) étant une base orthonormé, si on démontre l'égalité vectorielle :

A_{1}.\overrightarrow{u}+B_{1}.\overrightarrow{w}+C_{1}.\overrightarrow{z}=A_{2}.\overrightarrow{u}+B_{2}.\overrightarrow{w}+C_{2}.\overrightarrow{z}

cela conduit à une triple égalité :

A_{1}=A_{2}\quad et\quad B_{1}=B_{2}\quad et\quad C_{1}=C_{2}

Posté par
lidlkidjoere : Joint de Cardan 16-01-21 à 13:59

Merci vanoise, du coup j'aurais trois égalités . Mais alors si on me demande de faire le rapport \dfrac{\Omega}{\dot{Psi}}  

Il me reste pour l'égalité sur \overrightarrow{w}

\dfrac{\Omega}{\dot{\Psi}} = \dfrac{sin\theta}{sin\phi}

C'est ça que je dois comprendre ?

Posté par
vanoisere : Joint de Cardan 16-01-21 à 14:04

Oui !

Posté par
lidlkidjoere : Joint de Cardan 16-01-21 à 14:08

Et ce serait le loi de vitesse entrée/sortie du joint de Cardan si je prolonge avec les deux autres égalités ?

Posté par
vanoisere : Joint de Cardan 16-01-21 à 14:30

Sans énoncé complet, difficile d'être catégorique mais, a priori, tu as ta loi d'entrée - sortie. Si je comprends bien le problème : la vitesse d'entrée est \dot{\Psi} , la vitesse de sortie est ...

Posté par
lidlkidjoere : Joint de Cardan 16-01-21 à 14:37

Oui c'est bien comme ça que c'est organisé. La question que je recopie au dessus est exactement la question qui nous est posée. Pour les figures planes, elles sont vérifiées.
Merci pour ton aide.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !