Inscription / Connexion Nouveau Sujet
inventaire des forces
Bonjour tout le monde,
est ce que vous pouvez me corriger cet exercice que j'ai fait s'il vous plaît.
par contre j'ai du mal à répondre au question n 4.....Merci d'avance pour votre aide..
Une barre homogène AB de masse m et de longueur L s'appuie, d'une part en A sur un mur
1-Faire l'inventaire des forces qui s'exercent sur la barre AB et exprimer la relation
vectorielle qui traduit l'équilibre de cette barre. Ecrire les équations qui résultent de la
projection de la relation vectorielle sur les axes C x et C y .
2-Ecrire le théorème des moments par rapport au point C .
3-En déduire les valeurs de alpha.
4- Application numérique : l=1m , d= 0.4m , m=2kg , g=9.8 , . Calculer α et les intensités des réactions sur le mur et sur l'appui.
La barre étant en équilibre, les lignes de forces doivent être concourantes.
La barre AB est soumise à trois forces :
FA : la force exercée par l'axe sur la barre
FC : La force perpendiculaire à la barre exercée par le point C.
Le poids P concentrée au milieu G de la barre AB suivant y =Py
Au niveau de l'angle α, le mur exerce une force Ax qu'est perpendiculaire au mur
Pour les directions des force, seule la composante verticale de la force en C peut compenser le poids, puisque la force du mur est horizontale, et cette dernière doit compenser la composante horizontale en C.
La première condition d'équilibre conduit à l'équation vectorielle :
∑_(F ext= 0)
Soit :
Py + FA + FC =0
Relation qui, par projection sur les axes, donne deux équations algébriques :
Projection sur Cx : 0 + XA - FC cos(α)= 0
Projection sur Cy : -P + YA + FC sin(α)= 0
Cx = -C.cos(α)
Cy = C.sin(α)
Cy - Py = 0 donc C.sin(α) = Py
Et
Ax - C.cos(α) = 0 donc Ax = C.cos(α) = Py/ tang(α)
2
La barre étant en équilibre le moment en C, la force C donne un moment nul et il reste :
Le moment dû à A :
M(A) = d*Ax*cos(a)
le moment du au poids :
M(P) = (l*sin (a)/2 - d) *Py
L'annulation du moment total nous donne :
d*Ax*cos α = (l*sin (α)/2 - d) *Py
et en remplaçant Ax par sa valeur :
d*P*cos α / tang(α) = P*l*sin (α)/ 2 - d*P
Après simplification il vient une relation entre l'angle, d et l :
d*(cos2 α + sin α) = (l/2)*sin2 α
3-En déduire les valeurs d'alpha.
C.cos(α) = Py/ tang(α)
Tang (α) = Py/ C.cos(α
Bonjour
Une barre homogène AB de masse m et de longueur L s'appuie, d'une part en A sur un mur
La phrase est incomplète : faut-il comprendre que la tige est mobile sans frottement autour d'un axe horizontal, passant par C, perpendiculaire au plan de figure ?
Autres questions :
1° : Est-il précisé que l'action de la paroi sur la tige en A se fait sans frottement. Si non, il faut envisager pour cette action une composante normale (horizontale) et une composante tangentielle due aux frottements.
2° : La distance AC est-elle fournie ?
bonjour vanoise ,
Je vous remercie pour votre réponse....
je suis désolée de cette erreur.. voici l'énoncé rectifié :
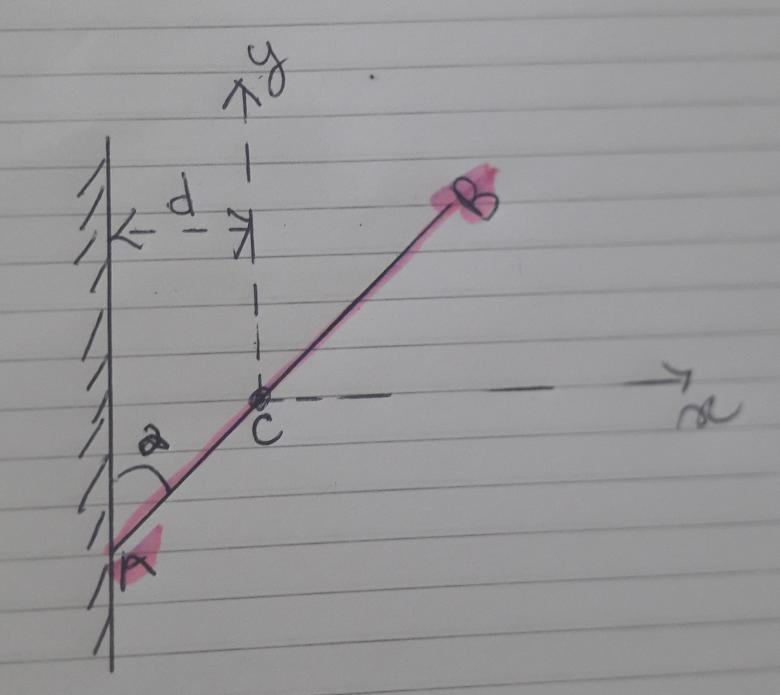
Une barre homogène AB de masse m et de longueur L s'appuie, d'une part, en A sur un mur, et d'autre part , en C sur un appui situé à une distance d de celui-ci . on appelle α l'angle entre la barre AB et le mur. On suppose que les laissions sont sans frottements. On définit un système d'axes Cxy comme figuré sur le schéma.
1-Faire l'inventaire des forces qui s'exercent sur la barre AB et exprimer la relation
vectorielle qui traduit l'équilibre de cette barre. Ecrire les équations qui résultent de la
projection de la relation vectorielle sur les axes C x et C y .
2-Ecrire le théorème des moments par rapport au point C .
3-En déduire les valeurs de alpha.
4- Application numérique : l=1m , d= 0.4m , m=2kg , g=9.8 , . Calculer α et les intensités des réactions sur le mur et sur l'appui.
et bien entendu l'absence de frottement signifie que les réactions sont perpendiculaires aux appuis.
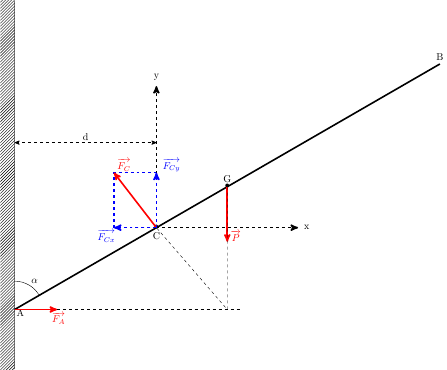
Merci pour les précisions. Le schéma complété devrait ressembler à ceci...
Raisonner sur le fait que les trois forces sont concourantes est possible mais il est plus simple d'utiliser la méthode proposée par l'énoncé.
La somme des moments en C est nulle : cela te donne l'expression de l'intensité FA en fonction du poids, de  et des distances.
et des distances.
Le fait que la résultante des trois forces soit le vecteur nul conduit simplement à :
FCx=FA
FCy=m.g
bonjour vanoise,
donc les intensités des réactions sur le mur et sur l'appui?
La barre est en équilibre et immobile : cela signifie que la résultante des forces qui s'exercent sur elle est nulle et que rien ne la fait tourner.
Les forces qui s'exercent sur elle :
. Appliquée au point G, le poids (direction verticale, sens vers le bas, intensité 2x9.80 N)
. Appliquée au point C, une réaction du support (direction verticale, sens vers le haut, intensité ? )
. Appliquée au point A, une force exercée par le mur ,une force qu'est perpendiculaire au mur qui tient la masse AB et C (direction horizontale , sens vers la droite, intensité = mAB.g + mC.g )
Bonjour
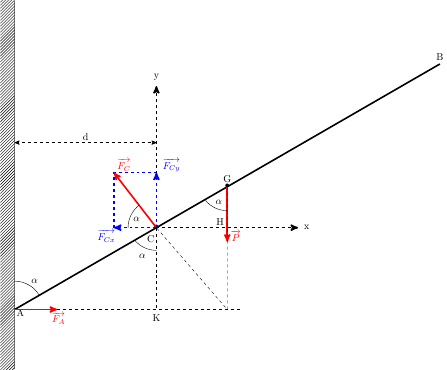
Ton deuxième message est beaucoup plus précis ; il n'y a pas de liaison pivot passant par C mais un simple appui sans frottement. Il est ainsi inutile de fournir la distance AC mais le problème demande un peu d'agilité en trigonométrie...
En raisonnant sur les produits vectoriels ou sur la notion de bras de levier, le théorème des moments statiques appliqué en C conduit à :
Le théorème des moments statiques en C conduit finalement à :
L'appui en C étant sans frottement, Le vecteur force est orthogonal à la tige AB. Ce qui conduit à :
En identifiant les deux expressions de FA et en simplifiant par m.g :
Au final :
Application numérique :
La suite est facile...
bonjour vanoise
Peux-tu vérifier stp les réactions:
Rc=mg/(sin a) =2x9.8/sin68 = 21 N
RA = RC cos α = 21 cos 68 = 7.80 N



