Bonjour.

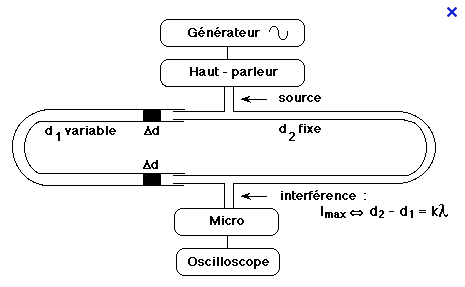
Le trombone de Koenig est un dispositif de laboratoire permettant de faire interférer deux ondes sonores ayant suivi des chemins différents. Le haut- parleur, alimenté par un générateur de basse fréquences, émet un son de fréquence f=1500 Hz . On mesure le signal à la sortie avec un microphone branché sur un oscilloscope . En déplaçant la partie mobile on fait varier l'amplitude du signal observé. Elle passe deux fois de suite par une valeur minimale lorsque l'on déplace d1 de d=11,5cm 2mm .

Déterminer la valeur de ma célérité du son dans l'air à 20°C, température à laquelle l'expérience est faite .

Mon problème c'est que, j'ai vu quelques part que la différence de marche est =11,5×2 cm.. Pouvez vous m'expliquer cela car je sais que =d2 -d1=k car on a des interférences constructives