Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Interférences

Posté par
alouette13 30-09-17 à 16:13

Bonjour !

Je dois démontrer dans le cas où les ondes émises sont en en phase, le déphasage entre les 2 ondes reçues en M s'écrit = (2/) * a sin .

Mais je ne vois pas comme faire

Posté par
vanoisere : Interférences 30-09-17 à 16:36

Bonjour
Tu ne décris pas le dispositif optique utilisé ! Impossible de fournir une réponse précise !
Une indication tout de même : il faut déterminer la différence de marche entre les deux ondes interférant en M. En notant L cette différence de marche, on obtient ensuite :

\Delta\varphi=\frac{2\pi}{\lambda}\cdot\Delta L
Tu es donc amené à démontrer :

\Delta L=a\cdot\sin\left(\theta\right)

Posté par
alouette13re : Interférences 30-09-17 à 16:51

On note a la distance entre les 2 émetteurs E1 E2,  et O le milieu du segment E1 E2. Et M est le récepteur

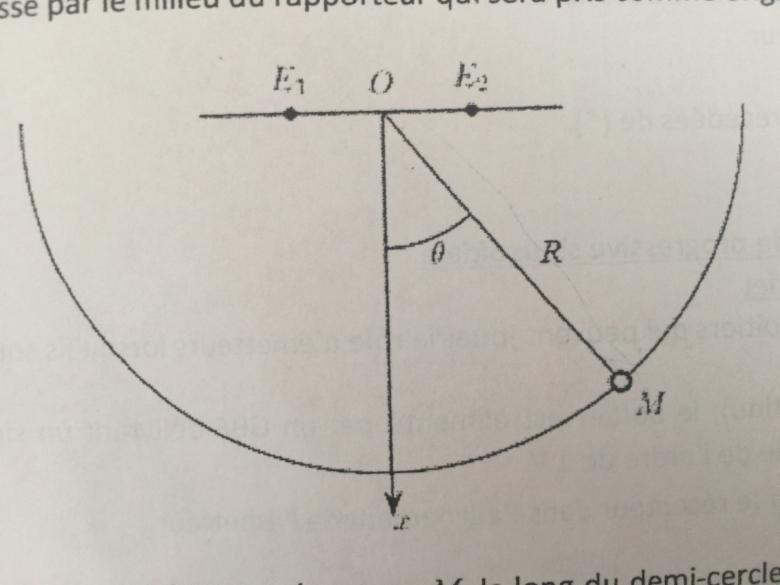
Interférences

Posté par
vanoisere : Interférences 30-09-17 à 17:47

La méthode consiste à utiliser le théorème d'Al Khashi aux triangles (E1MO) et (E2MO) pour exprimer \Vert\overrightarrow{E_{1}M}\Vert^{2} puis \Vert\overrightarrow{E_{2}M}\Vert^{2} en fonction de \theta; R et (a/2) puis à simplifier en effectuant un développement limité en (a/R) sachant qu'en pratique : a<<R.

Posté par
alouette13re : Interférences 30-09-17 à 18:13

Merci pour votre réponse, pouvez vous m'aider sur ma résolution ?

Donc (norme E1M)^2 = R^2 + (a/2)^2 - 2(R*(a/2))*cos

Mais comment faire apres ? Je ne connais pas le développement limité

Posté par
alouette13re : Interférences 30-09-17 à 18:14

Et comment faire le lien avec le déphasage et  la longueur d'onde?

Posté par
vanoisere : Interférences 30-09-17 à 19:45

Pour ta deuxième question : je t'ai fourni le résultat ; la démonstration est sûrement dans ton cours. Sinon :

\Vert\overrightarrow{E_{1}M}\Vert^{2}=R^{2}+\frac{a^{2}}{4}-R.a.\cos\left(\frac{\pi}{2}+\theta\right)=R^{2}+\frac{a^{2}}{4}+R.a.\sin\left(\theta\right)
\\ \Vert\overrightarrow{E_{1}M}\Vert^{2}=R^{2}\left[1+\frac{a^{2}}{4R^{2}}+\frac{a}{R}\cdot\sin\left(\theta\right)\right]\quad;\quad\Vert\overrightarrow{E_{1}M}\Vert=R\left[1+\frac{a^{2}}{4R^{2}}+\frac{a}{R}\cdot\sin\left(\theta\right)\right]^{\frac{1}{2}}

En effectuant un développement limité au premier ordre en a/R :

\Vert\overrightarrow{E_{1}M}\Vert\approx R\left[1+\frac{a}{2R}\cdot\sin\left(\theta\right)\right]

Je te laisse continuer...
Remarque : le calcul est assez analogue à celui permettant d'obtenir le potentiel créé par un dipôle électrostatique... Mais tu n'as peut-être pas encore étudié cela...

Posté par
alouette13re : Interférences 01-10-17 à 10:44

Merci !
Peut on dire que vu que a<<R
Alors on a L=sin a ?
Non effectivement je n'ai pas encore vu ce calcul

Posté par
vanoisere : Interférences 01-10-17 à 12:13

Selon toi, une longueur pourrait être égale à un sinus ? De plus le sinus d'une longueur et non d'un angle ...
Tu donnes vraiment l'impression de t'être lancé dans la résolution de cet exercice sans t'être donné la peine d'étudier avant le cours sur les interférences de façon approfondie. Dans ces conditions, te fournir un corrigé ne serait pour toi d'aucune aide véritable à long terme...
Sur  le modèle que je t'ai fourni, calcule la valeur approchée de la norme du vecteur E2M . La différence de marche est alors la différence des distances E1M et E2M... Je t'ai fourni la réponse dans mon message du   30-09-17 à 16:36...

Posté par
alouette13re : Interférences 01-10-17 à 15:11

Oui pardon..

Norme E2M=R^2 - (a/2)^2 + 2E2M*(a/2)*cos et apres je fait la différence des 2, et je dois trouver sin a ?

Posté par
vanoisere : Interférences 01-10-17 à 15:37

Puisque tu ne domines pas le théorème d'Al Khashi, tu peux écrire :

\overrightarrow{E_{2}M}=\overrightarrow{E_{2}O}+\overrightarrow{OM}

On élève au carré :

\Vert\overrightarrow{E_{2}M}\Vert^{2}=\Vert\overrightarrow{E_{2}O}\Vert^{2}+\Vert\overrightarrow{OM}\Vert^{2}+2\overrightarrow{E_{2}O}\cdot\overrightarrow{OM}

\Vert\overrightarrow{E_{2}M}\Vert^{2}=\frac{a^{2}}{4}+R^{2}+a.R.\cos\left(\overrightarrow{E_{2}O},\overrightarrow{OM}\right)=\frac{a^{2}}{4}+R^{2}+a.R.\cos\left(\frac{\pi}{2}+\theta\right)

\Vert\overrightarrow{E_{2}M}\Vert^{2}=\frac{a^{2}}{4}+R^{2}-a.R.\sin\left(\theta\right)

On remarque que, par rapport au calcul de (E1M), il suffit de remplacer \sin\left(\theta\right) par -\sin\left(\theta\right). Inutile donc de refaire tout le calcul. On obtient directement l'expression approchée :

\Vert\overrightarrow{E_{2}M}\Vert\approx R\left[1-\frac{a}{2R}\cdot\sin\left(\theta\right)\right]

D'où l'expression approchée de la différence de marche :

\Delta L=\Vert\overrightarrow{E_{1}M}\Vert-\Vert\overrightarrow{E_{2}M}\Vert\approx a.\sin\left(\theta\right)

Je te laisse réfléchir à tout cela mais, encore une fois, il te faut vraiment étudier et comprendre un cours précis et structuré sur ce sujet avant d'aborder les exercices...

Posté par
alouette13re : Interférences 01-10-17 à 16:41

Oui je vais reprendre mon cours pour mieux comprendre, merci en tout cas


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !