Niveau licence

Interference / coherence spatiale

Posté par
Mathieu95670 10-11-17 à 17:27

Bonjours, merci a vous pour votre attention.

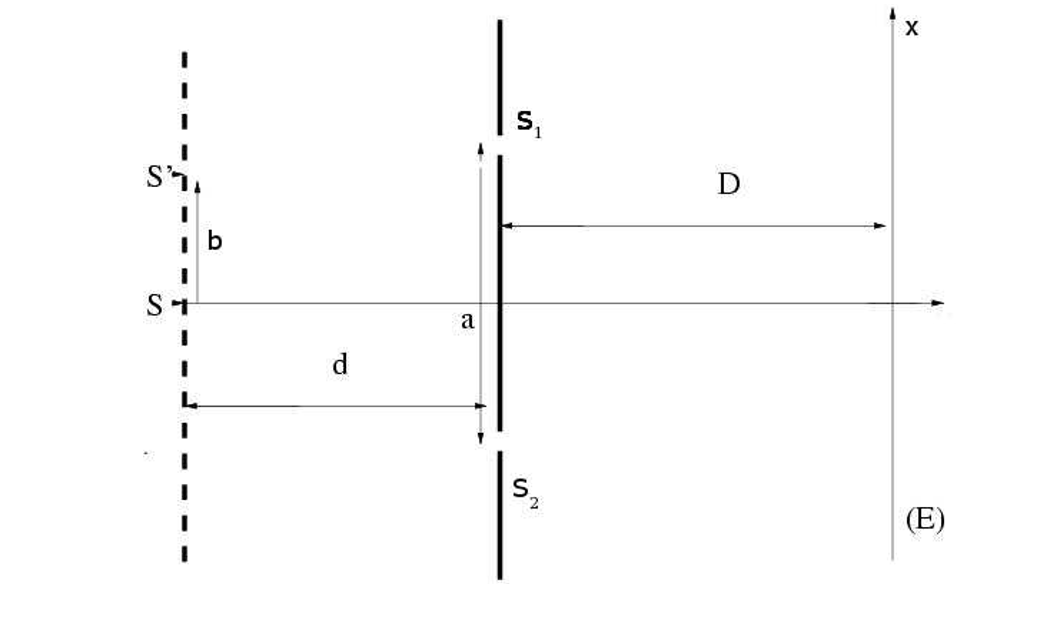
Je n'arrive a comprendre le résultat d'un exo,les source S et S' sont monochromatique de même longueur d'onde, on nous demande de trouver I(x,t), pour un x sur l'axe O'x
avant on a déjà trouver les intensité de chaque une séparément
$I(x)=I_{0}.sin^{2}(kax/2d)$
$I(x)=I_{0}sin^{2}(\frac{ka}{2}(\frac{b}{d}+\frac{x}{D}))$

au debut j'ai pris le module de la somme des fonctions d'ondes mais cetait enorme du coup j'ai arretter pour voir la solution et je comprend pas comment il peuvent trouver cela. $4I_{0}.[1+cos(\pi ab/\lambda d)cos(\frac{2\pi ax}{\lambda D}+\frac{\pi ab}{\lambda d})$

merci a vous. Bonne soirée

Interference / coherence spatiale

Posté par re : Interference / coherence spatiale 10-11-17 à 18:24

Bonsoir
Lorsque tu disposes de deux sources distinctes de même longueur d'onde, deux cas sont envisageables :
1° cas : elles sont cohérentes, cela veut dire qu'elles sont issues d'une même source primaire. Dans ce cas, les deux ondes peuvent interférer : le signal lumineux "s" en un point M donné est la somme des signaux s1 et s2 que créeraient en M chacune des sources séparément. On obtient l'intensité lumineuse en considérant qu'elle est proportionnelle au carré de l'amplitude de s.
2° cas : elles sont incohérentes ; elles ne peuvent interférer ; comme elles sont tout de même de même longueur d'onde, l'intensité lumineuse en M est la somme des deux intensités en M produites séparément par chacune des deux sources.
C'est la situation que tu as ici.

$I(x)=I_{1}(x)+I_{2}(x)$

Petit formulaire de math :

$\sin^{2}\left(\alpha\right)=\frac{1}{2}\left[1-\cos\left(\alpha\right)\right]$

$\cos\left(a\right)+\cos\left(b\right)=2\cdot\cos\left(\frac{a+b}{2}\right)\cdot\cos\left(\frac{a-b}{2}\right)$

Posté par re : Interference / coherence spatiale 10-11-17 à 18:42

$\sin^{2}\left(\alpha\right)=\frac{1}{2}\left[1-\cos\left(2\alpha\right)\right]$

Posté par re : Interference / coherence spatiale 10-11-17 à 18:45

Merci dirac ! J'ai beau me relire, les fautes de frappe sous Tex...

Posté par re : Interference / coherence spatiale 10-11-17 à 19:42

Merci beaucoup Mr Vanoise.
Donc si les ondes ne son pas coherente je peut sommer l'intensité sa je note .
Je mettait tromper au debut c'est des cos^2 pas des sin^2 .

Merci encore sa maide beaucoup

Posté par re : Interference / coherence spatiale 10-11-17 à 19:47

Enfin je comprend pas pourquoi je peut sommer les intensité... Vous auriez un document montrant cela a me partager ?

Merci

Posté par re : Interference / coherence spatiale 10-11-17 à 19:49

Citation :
c'est des cos^2 pas des sin^2 .

Dans ces conditions :

$\cos^{2}\left(\alpha\right)=\frac{1}{2}\left[1+\cos\left(2\alpha\right)\right]$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Interference / coherence spatiale

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique