Inscription / Connexion Nouveau Sujet
intéraction de deux courants filiformes
Bonjour,
J'aimerais que vous m'aidiez à comprendre un exercice qui me pose problème:
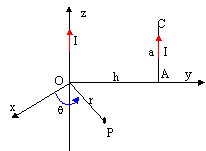
Un fil rectiligne de longueur infinie et de section négligeable est disposé suivant l'axe Oz du repère. Il est parcouru par un courant continu d'intensité I qui circule dans le sens de z positif.
J'ai montré que comme le champ magnétique B est orthoradial on a d'après le théorème d'Ampère B(M)= 0I/2
0I/2 r
r
C'est après que j'ai des soucis. On me dit qu'un second fil rectiligne de longueur a et de section négligeable est disposé dans le plan (xOy) selon le segment AC parallèle à Oz à la distance h de cet axe. Il est parcouru par un courant continu d'intensité I. Définir la résultante F des forces de Laplace qui s'exerce sur AC.
Je pensais faire dF=Idl B
B
dl=dz.ez (en gras j'écris les vecteurs) mais après B,je ne peux pas le prendre au point M si je veux inclure la distance h je dois le prendre selon A. Enfin en gros je ne sais pas trop quoi faire avec B
Merci pour vos réponses
Bonjour,
Tu connais dl, B et I. Tu as juste à faire le calcul, il n'y a plus de difficulté. Enfin, rappel, au centre, tu as un champ nul engendré par le fil fini.
J'ai dF=Idzez^Be
Je ne peux pas assembler les vecteurs polaires de B et les vecteurs du plan c'est ça qui me pose problème, je dois exprimer B selon quel axe? y ou x ? et pourquoi ?
Il n'y a pas de x et de y. Tu continues de travailler en polaire, tout simplement.
Tu as dF = IBdz.vect(ez)^vect(etheta). Il te reste à intégrer sur le fil fini, tu vois ?
Oui et non, je vois que je travaille en polaire, j'ai donc dF=IBdzvect(ez)^vect(e )
)
On en reviens toujours au même problème pour moi ce fichu produit vectoriel
vect(ez)=(0,0,1) vect(e )=(?) En fait je crois que je confonds tout, je suis perdue!
)=(?) En fait je crois que je confonds tout, je suis perdue!
Je vois ton problème.
Tu sais que qu'un coordonnées cylindrique (polaire en 3D), Ur, Ut et Uz forment un trièdre direct. Donc, vect(ez)^vect(e ) = -vect(ur). Voilou^^
) = -vect(ur). Voilou^^
Oui pardon ce sont des vecteurs, mais peut-on écrire que (je prends ur,ut et uz pour vecteurs polaires)
ur(1;0;0)
ut(0;1;0)
uz(0;0;1) et donc uz^ut=-ur parce que en faisant le produit vectoriel avec les coordonnées je trouve -1? Cette écriture étant juste pour moi pour me repérer plus facilement je ne le mettrai pas dans une copie. Parce que là on n'a pas d'angle à prendre en compte mais si on en avait eu un on aurait du remplacer le 1 par cos par exemple.
par exemple.
il vaut mieux retenir ce que je t'ai dit. Car ce que tu écris en est une conséquence directe et non l'inverse. Par contre, oublie ton histoire d'angle, ça me semble pas très clair tout ça. Il définit quel angle, ce alpha ?
Peux tu finir le calcul ou tu bloques ?
Pour le calcul où je bloquais je crois que c'est :
dF=I*(I 0/2
0/2 h)*dz(-ur)
h)*dz(-ur)
F=-I2 0/2
0/2 h
h dz.ur intégrale entre 0 et a, donc
dz.ur intégrale entre 0 et a, donc
F=-I2 0*a/2
0*a/2 h.ur
h.ur
Je pense que c'est ça car j'intègre l'élément de courant dz sur la longueur du fil fini.
Pour mon histoire d'angle c'est parce que j'ai retrouvé un exercice où j'avais dB= 0/4
0/4 *IDL^ur/r2
*IDL^ur/r2
En figure j'ai un fil de longueur A1-A2 parcouru par I et H le projeté orthogonal de M sur le fil. Il est écrit que dl=(0;0;dz) et ur=(cos ;0;-sin
;0;-sin ) où
) où  est l'angle entre HM et MA2
est l'angle entre HM et MA2
et ensuite dl^ur=(0;dzcos ;0)
;0)
Voilà pour mon histoire d'angle
Si tu remplaces 2*pi*h par (2*pi*h) (priorité des parenthèses sur la division). En effet, le vecteur est au numérateur, on ne divise jamais par un vecteur, ça n'a pas de sens.
Ne mélange pas tout ! On introduit des angles que s'il y a besoin, tu mélanges des méthodes d'exos différents. Et puis, ta formule est la loi de Biot et Savart, c'est pas la même chose, même si tu as un produit vectoriel.
Cela étant dit, tu as l'air d'avoir compris ce calcul, mais soit plus rigoureuse dans les notations, oki ?
Je dois aussi calculer le moment M(O) en O des forces de Laplace qui s'exercent sur le fil AC.
Chose que j'adore je n'ai pas de cours sur le moment cinétique donc vive internet qui me dit que le moment en un point O de la force F exercée en P est : Mo(F)=OP^F
Donc si je me reporte à mon exercice M(O)=OM^F
J'écris un peu OM au pif parce que je ne sais pas si ce ne serait pas plutôt OA puisqu'on veut les forces qui s'exerce sur le fil, le point M n'est pas sur le fil mais ça me fait bizarre OA...
Oui je serais plus rigoureuse désolée. c'est vrai je mélange un petit peu tout, j'ai vraiment du mal avec tout ce qui est projection et visualisation dans l'espace, enfin c'est de l'entraînement! avec de la pratique ça finira bien par rentrer!
En effet, le moment d'une force centrale s'écrit vect(mo(M)) = vect(OM)^vect(F).
Tu viens de calculer vect(F) et vect(OM) est facile à exprimer, c'est de la géométrie. Peux tu me le faire ?
Alors on a vu que vect(uz)^vect(ut)=-vect(ur) (je reprends ur; ut et uz plus simples à écrire que e ...)
...)
Pour vect(OM) il faut que j'exprime vect(OM) en fonction de ut et uz, sur ut j'ai h*vect(ut) par contre sur uz je ne vois pas trop comment faire, je suis tentée de dire que j'aurais z*vect(uz) mais c'est plus parce que je n'ai que z de défini sur cet axe qu'autre chose...
Cela me donne vect(OM)=h*vect(ut)+z*vect(uz)?
PS : j'ai pris M en (h,0,0) en considérant l'extrémité du fil. Mais il serait de bon ton de prendre le barycentre du fil fini.
Euh, c'est des maths.
Regarde ou son les vecteurs sur ce dessin. http://wiki.sillages.info/index.php/Vecteur_vitesse_et_acc%C3%A9l%C3%A9ration_en_coordonn%C3%A9es_cylindriques
(Expliquer les coordonnées cylindriques me prendra des heures à taper, donc, je garde ça en dernier recours).
Ok, je crois que j'ai compris pour les coordonnées cylindriques, il faudra que je pratique encore un peu.
j'ai donc vect(OM)^vect(F)= hvect(ur)^-( *I2*a/2
*I2*a/2 h)*vect(ur)
h)*vect(ur)
(je mets =
= 0 ça fait plus propre et plus simple à lire)
0 ça fait plus propre et plus simple à lire)
Le problème c'est que vect(ur)^vect(ur)=0
Mon moment ne peut pas être égal à zéro ou alors j'ai encore rien compris et là tu es en train de te tirer les cheveux!
Si, tu as bien compris le calcul. Mais, c'est pour la base. Je pense (mais là, il faudrait que je voie le sujet en entier, parce que je commence à avoir du mal à voir où le sujet nous emmène), qu'il faut prendre le barycentre du fil et donc en M (h,0,a/2).
Le début du sujet est dans mon premier post la première question était de déterminer le vecteur champ magnétique B(M) crée au point M. Chose faite ça ne m'a pas posé de problème.
Deuxième question, un second fil rectiligne de longueur a et de section négligeable est disposé dans le plan (xOy)selon le segment AC parallèle à Oz, à la distance h de cet axe. Il est parcouru par un courant continu d'intensité I. Définir la résultante F des forces de Laplace qui s'exercent sur AC, chose faite aussi maintenant.
3) Déterminer le moment cinétique M(O) en O des forces de Laplace qui s'exercent sur le fil AC.
4)Déterminer dans ces conditions la distance b qui sépare le point A du point K de AC, point où la force unique F peut être considérée comme appliquée à AC.
Voilà pour l'énoncé avec le superbe schéma que j'ai mis dans mon premier post.
Ok, je vois maintenant. Je tape la réponse demain. Je vais me coucher (et vu mes performances du jour, je crois qu'un peu de repos me fera du bien^^).
@demain.
J'osais pas te le dire que moi aussi j'aurais bien été au dodo un petit peu histoire de digérer tout ça. En tout cas merci déjà pour tout ce qe tu m'as expliqué. A demain !
Bonjour,
Alors après une bonne nuit de sommeil, j'ai regardé une nouvelle fois le sujet et je n'ai pas compris pourquoi dans le sujet que je t'ai envoyé les réponses étaient pour vect(OM)=-hvect(ut)+zvect(uz)?
Bonsoir,
(Je suis entrain de me faire à manger, je viens de rentrer). Donc, je peux ne pas répondre toujours rapidement.
Deja, dans la correction de Chimix, c'est vect(OP) avec P app à [AC].
Et c'est en coordonnées carthésienne. vect(OP) = h.vect(uy) + z.vect(uz) avec z app à [0,a].
En coordonnée cylindrique, ça serait : vect(OP) = h.vect(ur) + z.vect(uz) (et une compososante quelquonque sur théta que l'on peut prendre à zéro si on astucieux).
Normalement, on fait plutôt l'exo en polaire à cause du champ orthoradiale. Mais vu que le segment est figé. Tu peux facilement exprimer les vecteurs en coordonnées carthésienne si tu n'es pas à l'aise en cylindrique.
Pas de soucis j'attends, je ne suis pas pressée l'essentiel pour moi c'est de comprendre.
Je comprends qu'on peut exprimer en carthésien mais pourquoi eux ils mettent -h ?
Et z est une projection de OP sur AC et ccomme AC est parallèlle à Oz on peut exprimer z, non ?
Le moins vient de l'élément de force df (comme pour le calcul de F de la question 2)
Z est juste la coordonnée de P suivant uz, tout simplement.
Ok oui j'avais pas vu pour le moins, désolée.
Donc on se retrouve avec vect(OP)=hvect(ur)+zvect(uz)
Et comme vect(F) est suivant ur il ne nous reste que :
vect(mo(M))=vect(OP)^vect(F)= -zvect(uz)^dFvect(ur)
J'écris dF pour ne pas réécrire ce qu'on avait trouvé hier, ce qui m'intéresse surtout c'est de savoir si je ne me trompe pas dans les coordonnées.
Donc vect(uz)^vect(ur)=vect(ut) ?
Mais alors je vais avoir un moment négatif ? Si vect(uz)^vect(ur)=-vect(ut) je ne sais pas pourquoi.
Ne mélange pas expression differentielle et leur relation d'origine.
Soit tu connais le point d'application K et la force et tu utilises directement vect(Mo(F)) = vect(OK)^vect(F). Mais c'est ce que l'on te demande à la question 4) (tu comprends pourquoi je voulais voir tout le sujet).
Toi, tu dois utiliser la forme différentielle à savoir.
d[vect(Mo(F)](P) = vect(OP)^vect(dF)
Que tu intègres sur l'ensemble des P app à [AC].
Donc, d[vect(Mo(F)](P) = vect(OP)^vect(dF) = (h.vect(ur)+z.vect(uz))^(I.dz.vect(uz)^vect(B)) = (h.vect(ur)+z.vect(uz))^(I.dz.vect(uz)^(I²µo)/(2pi*h).vect(ut))
On a vect(uz)^vect(ut) = -vect(ur) (le moins), vect(ur)^vect(ur) = 0 et vect(uz)^vect(ur) = vect(ut)
d[vect(Mo(F)](P) = -(I²µo)/(2pi*h).z.dz.vect(ut)
Est ce que tu comprends jusque là ?
Oui je comprends jusque là, tu as juste mis un I au carré en trop je crois dans l'expression de B.
Mais oui jusque là je comprends. j'ai compris pour les coordonnées. Après pour avoir le moment j'intègre entre 0 et a.
Ensuite pour trouver la distance b qui sépare le point A du point K de AC point où la force unique F peut être considérée comme appliquée à AC.
Il y a un truc que je ne comprends pas c'est que F on l'applique déjà à AC? puisque c'est ce qu'ils nous demandent à la question 2.
En effet, on intègre en 0 et a pour avoir le moment. Par contre, c'est bien des I² (comme dans la correction).
Pour la dernière question, tu cherches le point d'application K tel que le moment calculé dans la question 3 est égal au moment de la résultante F, calculé à la question 2 en ce point K.
Donc, tu veux, Mo(F) = vect(OK)^vect(F).
Ce calcul sert à connaître le point d'application du moment pour pouvoir faire de la mécanique du point)
Ok je crois que j'ai compris. Je veux K tel que vect(OK)^vect(F)=Mo(F)=-(I²µo)a2.vect(ut)/(4pi*h)?
Mais je crois que j'ai du me tromper dans le calcul de l'intégrale car je trouve Mo(F)=-(I2µo)a2/(4 *h)
*h)
Je me laisse corrompre par la correction...
Donc, oui, c'est normal que tu aies un signe négatif en vect(ut) car vect(ux) = -vect(ut) dans cette configuration.
C'est bien ce que je pensais que c'était à cause de ut, donc tout va bien parce que si je repasse en coordonnées cartésiennes je retombe sur du positif, non?
A ma décharge, j'ai pas fait l'exo, je le fais de tête (donc, avec le temps entre les réponses, je me laisse influencer par la correction, qui a gardé les vecteurs carthésiens (je me demande pourquoi...)
C'est bien ce que je pensais que c'était à cause de ut, donc tout va bien parce que si je repasse en coordonnées cartésiennes je retombe sur du positif, non?
Oui car vect(ut) = -vect(ux). Il faut que tu fasses le dessin pour le voir. Mais c'est un cas particulier car les deux fils sont dans le plan (zOy). Avec le vecteur vect(ut), c'est toujours vrai même s'il n'est pas dans ce plan.
Yes, c'est bon, j'ai compris, je n'ai plus qu'à refaire l'exercice demain et voir si ça passe! Merci beaucoup et le lien que tu m'as donné de wiki sillages m'a beaucoup aidé c'est très bien expliqué!
Merci, révise bien toi aussi, bon courage et à bientôt !
Si tu veux vérifier d'avoir bien compris demain, n'hésite pas.
Ce fut un plaisir de t'aider (ça me change, des élèves qui cherchent !).
Tu n'as pas de concours cette année, je suppose, mais bonne chance pour ta fin d'année.


