Bonjour
Connais-tu la théorie des torseurs pour modéliser les actions réparties ?
Il s'agit en fait de montrer que le moment de cette charge répartie possède un moment nul au milieu.

Non je connais pas cette théorie , ils nous le prouvent juste en intégrant et de là ils en déduisent la force résultante et sa position donc mathématiquement je comprends mais intuitivement je vois pas pourquoi

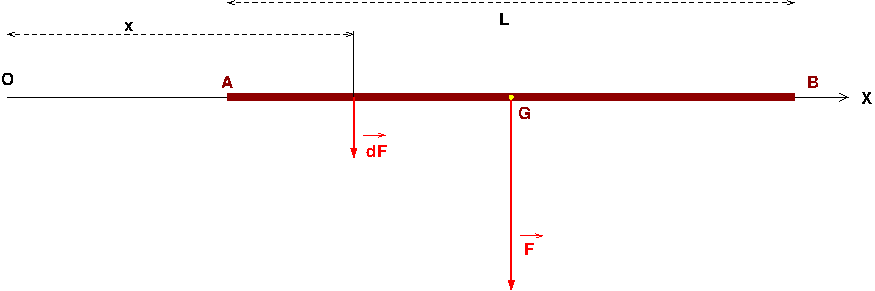
Je prends le cas simple d'une tige AB de longueur L, la charge par unité de longueur est f. La résultante  est donc F=f.L

En supposant la charge verticale et la tige horizontale (je simplifie). Je cherche à déterminer le moment en un point O de cette charge répartie. Un petit élément dx de tige situé à la distance x de O possède la charge f.dx. le moment  de cette charge élémentaire en O est :



Le moment résultant de la charge vaut :





Le moment en un point quelconque se calcule comme si la charge totale était appliquée au centre de la tige à condition que la charge soit uniformément répartie. Or les problèmes de statique et de dynamique font très souvent intervenir les moments.
Une démonstration générale suppose l'utilisation des produits vectoriels. J'ai simplifié à l'extrême.