Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Induction magnétique

Posté par
ThananaSplit 06-02-19 à 21:22

Bonjour,

J'ai quelques petits blocages sur un exercice de physique (sur les ondes électromagnétique), voici l'énoncé :

Un cadre conducteur de forme carré ABCD dr côté L abune résistance électrique R, une masse m et est soumis à son poids \vec{P}=-mg\vec{u_z}
. Le cadre se trouve dans le plan xOz, avec le côté AB confondu avec l'axe Ox à t=0. Un champ magnétique uniforme \vec{B}=B_0\vec{u_y}
règne dans le demi espace z<0. Le cadre est lâché à t=0, sans vitesse initiale.

a) déterminer l'expression de la force électromotrice (fem) induite dans le cadre, ainsi que le sens et la valeur du courant circulant dans celui-ci.

b) Déterminer la force de Laplace agissant sur le côté AB

c) Établir l'équation différentielle du mouvement du cadre selon Oz et déterminer l'expression de la vitesse du cadre en fonction du temps

____________________________________________________________________________________________

Voici ce que j'ai fais pour l'instant :

a) j'ai un soucis car je suis censé trouvé une expression du flux dépendant du temps t, or voilà ce que j'ai :

force électromotrice : e = -\frac{d\phi }{dt} avec \phi le flux : \phi = \int \int \vec{B}.\vec{dS} = \int \int \vec{B}.\vec{n}dS ou \vec{n} est un vecteur normal au cadre dirigé vers l'extérieur.
Mon calcul est : \phi = \int_{-L/2}^{L/2}{\int_{-L/2}^{L/2}{B_0dxdz}} = B_0L^2
ce qui me pose problème car je suis censé trouvé une expression du flux dépendant de t afin d'en déduire e...

b) Pas de problème pour cette question

c) Je dois partir du principe fondamental de la dynamique (seconde loi de Newton), et notre professeur nous a dit que l'on devait tombé sur équation différentielle du premier ordre. Or, quand je fais le bilan des forces : J'ai le poids, le champ magétique et la force de Laplace soit : \vec{P}+\vec{B}+\vec{F}=\frac{d\vec{p}}{dt}=m\vec{a}
et à partir de là, je ne vois pas comment exprimer \vec{a}. D'accord, c'est la dérivé seconde de la position mais même, je ne vois pas.

Merci d'avance pour votre aide.

Posté par
vanoisere : Induction magnétique 06-02-19 à 21:35

Bonsoir
Juste une aide rapide pour débloquer la situation.
Tant que le cadre n est pas entièrement dans le champ magnétique, la surface à prendre en compte est
S=L.x=L.v.t
Attention aux signes en fonction des orientations.  Un scan du schéma serait le bienvenu.

Posté par
ThananaSplitre : Induction magnétique 06-02-19 à 21:49

Effectivement c'est bête mais je n'y avais même pas pensé...

Le calcul serait donc : \phi = \int_{x=-L/2}^{x=L/2}{\int_{z=-L/2}^{z=Lvt}{dxdz}}= -B_0L\times (Lvt+\frac{L}{2})=-B_0L^2vt-\frac{B_0L^2}{2} , j'ai juste ?

Et pour la question c), je viens de me rendre compte qu'il ne faut pas prendre en compte le champ magnétique, comme l'énoncé demande selon Oz...?

Et voici le schéma que j'ai fais :

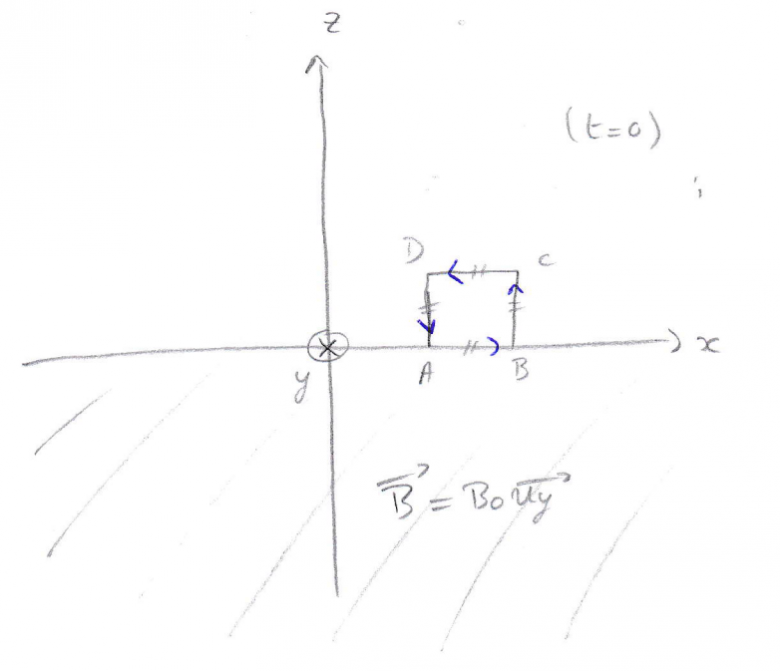
Induction magnétique

Posté par
vanoisere : Induction magnétique 06-02-19 à 22:23

Non ! Reprends ton calcul de S. Attention, je t'ai fait dans mon message précédent un calcul en supposant v constant, ce qui est faux dans le cas général que je développe ci-dessous.
Si tu notes z la cote du côté AB, le vecteur surface associé à la partie du cadre placé dans le champ magnétique est :

\overrightarrow{S}=L.z.\overrightarrow{u_{y}}\quad avec\quad z<0

Le flux magnétique à travers le cadre est :

\Phi=\overrightarrow{B}.\overrightarrow{S}=B.L.z

D'où la fém induite :

e=-B.L\frac{dz}{dt}>0

PS : soit ton professeur est maladroit, soit il est maso car orienter l'axe (Oz) vers le haut alors que le mouvement se fait vers le bas...

Posté par
ThananaSplitre : Induction magnétique 07-02-19 à 00:05

Je pense avoir compris, merci.

Toutefois j'ai toujours un problème pour établir mon équation différentielle à la question c. Selon (Oz), on a :
Le poids \vec{P}=-mg\vec{u_z} et la force de Laplace : \vec{F}=IB_0L\vec{u_z} (c'est ce que j'ai trouvé à la question b.

Mais de là je ne vois pas trop quoi faire...

Posté par
ThananaSplitre : Induction magnétique 07-02-19 à 00:12

Voici au cas où ce que j'ai fais pour la question b :

\vec{dF}=I\vec{dl}\wedge \vec{B}, sur AB : \vec{dl}=dx\vec{u_x} donc \vec{F} = \int_{-L/2}^{L/2}{IB_0dx}\vec{u_z}=IB_0L\vec{u_z}

Posté par
vanoisere : Induction magnétique 07-02-19 à 11:34

Pour c), la méthode générale comporte trois étapes :

1° : équation électrique : tu supposes le cadre en mouvement sans te préoccuper de ses causes (les forces) ; la loi de Pouillet ou tout autre méthode conduit à :

e=R.i   soit

-B.L\cdot v_{z}=R.i   (on néglige le phénomène d'auto-induction (l'inductance propre du cadre est supposée d'influence négligeable)

2° : équation mécanique : on applique les lois de la dynamique sans se préoccuper de la cause du courant induit :
\\ m.\dfrac{dv_{z}}{dz}=-m.g+B.L.i

3° : on fait la synthèse des deux études précédentes :

m.\dfrac{dv_{z}}{dz}=-mg-\dfrac{B^{2}.L^{2}}{R}\cdot v_{z}

Puisque vz<0, la force de Laplace est orientée vers le haut : c'est une force résistante, conformément à la loi de modération de Lenz.
Tu as bien l'équation différentielle vérifiée par la vitesse.

Posté par
ThananaSplitre : Induction magnétique 07-02-19 à 12:11

Ah oui ! Je n'avais pas fais le lien avec la première question...

J'ai donc essayé de résoudre cette équation, qui est de la forme " y' = ay +b" donc la solution est Ke^a^t-\frac{b}{a} avec ici : \frac{dv_z}{dt}=-\frac{B_0^2L^2}{mR}-g

Soit :  V_z(t) = Kexp(-\frac{B_0^2L^2}{mR})-\frac{gmR}{B_0^2L^2} ou K est une constante réelle.

Pour déterminer K, on regarde les conditions initiales, l'énoncé dit que le cadre est lâché sans vitesse initiale, donc V_z(t=0) = 0

Soit : K = \frac{gmR}{B_0^2L^2}

Et donc finalement : V_z(t) = \frac{gmR}{B_0^2L^2}\times exp(\frac{-B_0^2L^2}{mR}t)-\frac{gmR}{B_0^2L^2} = \frac{gmR}{B_0^2L^2}(exp(\frac{-B_0^2L^2}{mR}t)-1)

si je n'ai pas fais d'erreur ?

Posté par
vanoisere : Induction magnétique 07-02-19 à 13:39

Cela me  semble correct.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !