Bonjour à tous, je travail sur un exercice d'induction électromagnétique qui me pose problème..

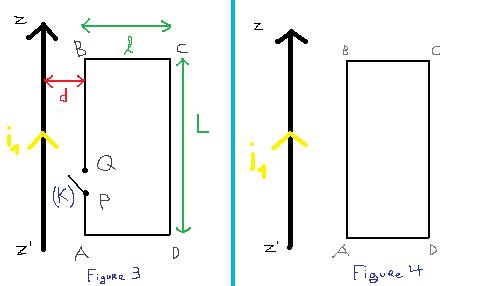
Dans le vide, un conducteur rectiligne d'axe zz' infiniment long est parcouru par un courant d'intensité i₁. Un cadre rectangulaire conducteur ABCD de longeur L=AB=CD, de largeur l=BC=AD est placé dans un plan contenant l'axe zz'. Le cadre ABCD est considéré comme purement résistif, de resistance R. Le côté AB, parallele à l'axe et (<= de est) situé à la distance d de la ligne de courant, comporte un interrupteur (K), de dimension négligeables, susceptible de fermer ou d'ouvrir le circuit au niveau de deux points P et Q très rapprochés (figure 3). Les conducteurs sont des fils cylindriques, de diamètre négligeable.

1. Flux du vecteur champ magnétique
a) L'espace est rapporté en coordonnées cylindriques à un repere de base (e_r,e,e_z). Etablir l'expression vectorielle du champ magnétique B₁(M) crée par le courant d'intensité i₁ en tout point M de l'espace situé à une distance r, non nulle, du conducteur filiforme.

=> Soit un point M quelconque, après étude vecteur B dépend que de r et est porté par z non ?
=> Loi de biot savart non ?

b) Préciser à l'aide d'un schéma, l'allure des lignes de champ magnétique.

=> je ne vois pas d'où part le champ et donc comment faire les lignes

c) Déterminer le flux du vecteur B(M) à travers le cadre rectangulaire ABCD

=> On calcule le flux, ça je sais faire

II. Force électromotrice et courant induit.
On étudit le dispositif précédent dans diverses situations.

1)PREMIER CAS: Le cadre est immobile, l'interrupteur K est fermé et le courant i₁=I₁ est constant et positif.
a) Existe-t-il une f.e.m (force électromotrice) e induite dans le cadre ? Si oui l'exprimer en fonction des données de l'énoncé.

=> Oui il existe une f.e.m e on la détermine à l'aide de la loi de faraday non ? mais dphi s'exprime comment ?

2)DEUXIEME CAS: le cadre est immobile et le courant d'intensité i₁ varie au cours du temps t, selon la loi i₁(t)=a.t+b.
a) L'interrupteur est fermé (figure 4). Recopier le dessin de la figure 4 en précisant le sens de la circulation du courant induit dans le cadre.

=> le courant va de la droite vers la gauche, soit dans le sens des aiguilles d'une montre non ?

b) Justifier le sens de circulation.

=> Comment justifier...

c) Exprimer, en fonction des données de l'énoncé, l'intensité i₂ de ce courant induit.

=> Partir de la loi de faraday non ?

d) L'interrupteur (K) est maintenant ouvert. Déterminer en fonction des données de l'énoncé, la différence de potentiel V_p-V_q existant entre les points P et Q.

=> Je part de quel formule ?


J'aimerai un peu d'aide de votre part, de vos suggestions, de vos idées, pour aider à avancer dans ce grand chapitre qui n'en fini plus, l'induction electromagnétique .
Merci cordialement de toute aide...