Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Induction de bobines sur l'axe

Posté par
lounastre 17-03-13 à 20:29

Bonsoir à tous,

je vous écris car j'aurais grand besoin d'aide pour cet exercice  =et j'espère que quelqu'un acceptera bien de m'aider :

Magnetisme

Champ d'une paire de bobines

Deux bobines circulaires d'axe Oz  et de rayon R=5 cm sont placées l'une en face de l'autre sur l'axe Oz a une distance R l'une de l'autre, de part et d'autre de l'origine O .

QCM 1

Ells sont parcourues par le meme courant, d'intensite I = +3A. La valeur algébrique du champ d'induction magnétique engendré à l'origine vaut :


A. 53,31  µT

B. 26,66  µT

C. 26,97  µT

D. 53,95  µT

E. 53,31 µT

QCM 2

On inverse le courant dans la bobine de droite   (z > 0). L'amplitude du champ d'induction magnétique sur l'axe au voisinage de l'origine, en fonction de z exprimé en cm, s'ecrit:

A.  12,95   z µT

B.  12,95   z mT

C.  -12,95  z µT

D.  26,66  z µT

E.  -26,66  z µT

Pour le premier QCM, il me semble quepour trouver l'induction de deux bobines en un point sur l'axe équidistant des 2 bobines, il y a une formule qui est la suivante : ((4/5)^3/2).(u0.n.I/R)

Par contre, pour la seconde question, je n'ai pas vraiment d'idée, je n'arrive pas à savoir quelle méthode appliquer ...

Merci d'avance à tous ceux qui quront la gentillesse de m'aider .

Posté par
lounastrere : Induction de bobines sur l'axe 18-03-13 à 12:22

S'il vous plait, est-ce que quelqu'un pourrait m'aider , ne serait-ce que me mettre sur la voie ou me confirmer mes hypothèses ?

Posté par
Aragornre : Induction de bobines sur l'axe 18-03-13 à 13:01

Bonjour,
Le champ magnétique sur l'axe d'une bobine plate doit être donnée par (sauf erreur de ma part) :
\Large B\,=\,\frac{\mu_0NI}{2R}\,\frac{R^3}{\left(R^2+d^2\right)^{\frac{3}{2}}}
Dans le cas ici,  d\,=\,\frac{R}{2}   si j'ai bien compris...
Mmais on ne connaît pas N...

Posté par
lounastrere : Induction de bobines sur l'axe 18-03-13 à 13:13

Merci beaucoup Aragorn d'avoir bien voulu jeter un oeil sur mon topic,

mais justement, au début je pensais utliser la meme formule que toi mais j'ai fati quelques recherches et, au funal, je suis tombée sur la formule que je propose dans le cas de deux bobines et de leur iduction à un point enune position qui s'appelle poistion d'helmotz et qui est une position sur l'axe et équidistante des deux bobines...

Pourriez-vous s'il vous plait confirmer ou infirmer mon hypothèse ...

Merci !

Posté par
Aragornre : Induction de bobines sur l'axe 18-03-13 à 14:30

Oui, effectivement, c'est exact...

Posté par
lounastrere : Induction de bobines sur l'axe 18-03-13 à 19:10

Merci beaucoup de ton aide argorn !

Sinon, en ce qui concerne la deuxièeme question, je dois t'avouer que je suis perdue !

Il me semble qu'il faut essayer de deriver par rapport à z l'expression suivante mais je n'en suis pas sure...

Si tu pouvais me donner un petit coup de main , ce serait gentil...

Posté par
Aragornre : Induction de bobines sur l'axe 18-03-13 à 23:04

Dans la 1ère question, les champs s'additionnent parce qu'ils sont de même sens.
Dans la 2ème, on inverse le courant dans une bobine. Les champs sont de sens opposé donc il faut soustraire les champs. Et je pense qu'il y aura probablement une histoire de développement limité autour de l'origine pour linéariser l'expression puisqu'on doit trouver une expression proportionnelle à z.
La dérivée n'apportera rien à mon avis (sauf pour le développement limité au 1er ordre).

\Large B\,=\,\frac{\mu_0NI}{2}\,\frac{R^2}{\left(R^2+d^2\right)^{\frac{3}{2}}}

Posté par
lounastrere : Induction de bobines sur l'axe 18-03-13 à 23:25

Merci beaucoup aragorn !

Le seul fait est que je ne sais pas quel développement limité adopter, je veux dire par là que je n'arrive pas à identifier la forme de la fonction de base : (1+x)^a, ou bien 1/1-x ...
Je ne sais pas trop ...

Merci d'avance !

Posté par
Aragornre : Induction de bobines sur l'axe 19-03-13 à 10:29

Je regarde ça d'un peu plus près...

Posté par
Aragornre : Induction de bobines sur l'axe 19-03-13 à 13:10

Le calcul n'est pas très difficile mais un peu long...
Je ne mettrai pas le calcul en entier mais les résultats principaux (détails sur demande expresse).
Je vais faire le calcul dans le cas général avec une distance d entre les bobines et, après, on fera d = R.
Avec les bobines disposées à la distance d symétriquement par rapport à l'origine, le champ magnétique sur l'axe dû à la bobine de droite (z > 0) s'écrit :
\Large B_1(z)\,=\,\frac{\mu_0NI}{2}\,\frac{R^2}{ \left(R^2+\left(\frac{d}{2}-z\right)^2 \right)^{\frac{3}{2}}}
En posant \Large K\,=\,\frac{\mu_0NIR^2}{2}, on peut écrire :
\Large B_1(z)\,=\,K\,\frac{1}{ \left(R^2+\left(\frac{d}{2}-z\right)^2 \right)^{\frac{3}{2}}}
\Large\boxed{ B_1(z)\,=\,K\,\left(R^2+\left(\frac{d}{2}-z\right)^2 \right)^{-\frac{3}{2}}}

De même, pour la bobine de gauche (z < 0) :
\Large B_2(z)\,=\,\frac{\mu_0NI}{2}\,\frac{R^2}{ \left(R^2+\left(\frac{d}{2}+z\right)^2 \right)^{\frac{3}{2}}}
Donc :
\Large\boxed{ B_2(z)\,=\,K\,\left(R^2+\left(\frac{d}{2}+z\right)^2 \right)^{-\frac{3}{2}}}

On va faire un développement limité dans les deux cas :
1) les bobines sont parcourues par le même courant (et disposées de la bonne façon ! ) donc les champs magnétiques s'ajoutent.
2) les bobines sont parcourues par des courants en sens inverse donc les champs magnétiques se soustraient.
Pour cela, il faut faire un développement limité selon z. Si on appelle B+ = B1 + B2 et B- = B1 - B2, le développement limité en z = 0 va s'écrire :
\Large \left(B_+\right)_{z=0}\,=\,B_+(0)\,+\,z\,\frac{dB_+}{dz}\left(0\right)\,+\,\frac{z^2}{2}\,\frac{d^2B_+}{dz^2}\left(0\right)
Et :
\Large \left(B_-\right)_{z=0}\,=\,B_-(0)\,+\,z\,\frac{dB_-}{dz}\left(0\right)\,+\,\frac{z^2}{2}\,\frac{d^2B_-}{dz^2}\left(0\right)
On a :
\Large \frac{dB_+}{dz}\,=\,\frac{dB_1}{dz}\,+\,\frac{dB_2}{dz}
Et :
\Large \frac{d^2B_+}{dz^2}\,=\,\frac{d^2B_1}{dz^2}\,+\,\frac{d^2B_2}{dz^2}
Et :
\Large \frac{dB_-}{dz}\,=\,\frac{dB_1}{dz}\,-\,\frac{dB_2}{dz}
Et :
\Large \frac{d^2B_-}{dz^2}\,=\,\frac{d^2B_1}{dz^2}\,-\,\frac{d^2B_2}{dz^2}
Donc il faut calculer  \Large \frac{dB_1}{dz} , \Large \frac{d^2B_1}{dz^2} , \Large \frac{dB_2}{dz} , \Large \frac{d^2B_2}{dz^2} .

La suite dans peu de temps...

Posté par
lounastrere : Induction de bobines sur l'axe 19-03-13 à 14:58

Merci beaucoup aragorn pour tout ce travail que tu as fourni , c'est impressionnant !

Néanmoins, j'aurais quelques questions à te poser : si on fait un développement d'ordre 1, la dérivéé première ne suffirait-elle pas à elle suele à faire le développement ?

D'autre part, je n'ai pas trop compris pourquoi considérer 2 cas de sens des courants alors qu'il me semble que l'énoncé dit plutot que les courants sont en sens inverse ?

Merci encore de ton aide !

Posté par
Aragornre : Induction de bobines sur l'axe 19-03-13 à 19:45

Dans le 1er cas, les bobines sont disposées de telle façon qu'avec le même courant, les champs magnétiques s'additionnent (vecteurs colinéaires de même sens). Dans le 2ème cas, on inverse le courant dans une bobine (bobine de droite) sans rien changer d'autre. Le champ magnétique de la bobine droite change de sens et est donc en sens opposé de celui de la bobine de gauche (qui a gardé le sens précédent). Dans ce cas, les champs magnétiques (colinéaires et de sens opposé) se soustraient.
Pour le développement limité, l'ordre 1 suffirait mais on ne peut pas le savoir avant...

\Large \frac{dB_1}{dz}\,=\,3K\left(\frac{d}{2}-z\right)\left[R^2+\left(\frac{d}{2}-z\right)^2\right]^{-\frac{5}{2}}
\Large \frac{d^2B_1}{dz^2}\,=\,3K\left[R^2+\left(\frac{d}{2}-z\right)^2\right]^{-\frac{5}{2}}\left[5\left(\frac{d}{2}-z\right)^2\left[R^2+\left(\frac{d}{2}-z\right)^{2}\right]^{-1}-1\right]

\Large \frac{dB_2}{dz}\,=\,-3K\left(\frac{d}{2}+z\right)\left[R^2+\left(\frac{d}{2}+z\right)^2\right]^{-\frac{5}{2}}
\Large \frac{d^2B_2}{dz^2}\,=\,3K\left[R^2+\left(\frac{d}{2}+z\right)^2\right]^{-\frac{5}{2}}\left[5\left(\frac{d}{2}+z\right)^2\left[R^2+\left(\frac{d}{2}+z\right)^{2}\right]^{-1}-1\right]

Il faut alors appliquer la formule du développement limité :
\Large \left(B_1+B_2\right)_{z=0}\,=\,K\left[R^2+\frac{d^2}{4}\right]^{-\frac{3}{2}}\,+\,z\,\,3K\frac{d}{2}\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\,+\,\frac{z^2}{2}\,\,3K\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\left[5\frac{d^2}{4}\left[R^2+\frac{d^2}{4}\right]^{-1}-1\right]\\ +\,K\,\left[R^2+\frac{d^2}{4}\right]^{-\frac{3}{2}}\,-\,\,z\,\,3K\frac{d}{2}\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\,+\,\frac{z^2}{2}\,3K\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\left[5\frac{d^2}{4}\left[R^2+\frac{d^2}{4}\right]^{-1}-1\right]
Donc :
\Large \left(B_1+B_2\right)_{z=0}\,=\,K\left[R^2+\frac{d^2}{4}\right]^{-\frac{3}{2}}\,+\,\frac{z^2}{2}\,\,3K\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\left[5\frac{d^2}{4}\left[R^2+\frac{d^2}{4}\right]^{-1}-1\right]\\ +\,K\,\left[R^2+\frac{d^2}{4}\right]^{-\frac{3}{2}}\,+\,\frac{z^2}{2}\,3K\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\left[5\frac{d^2}{4}\left[R^2+\frac{d^2}{4}\right]^{-1}-1\right]
\Large \left(B_1+B_2\right)_{z=0}\,=\,K\left[R^2+\frac{d^2}{4}\right]^{-\frac{3}{2}}\left[2\,+\,3z^2\left[R^2+\frac{d^2}{4}\right]^{-1}\left[5\frac{d^2}{4}\left[R^2+\frac{d^2}{4}\right]^{-1}-1\right]\right] \\
En arrangeant un peu l'expression :
\Large \left(B_1+B_2\right)_{z=0}\,=\,\frac{K}{\left[R^2+\frac{d^2}{4}\right]^{\frac{3}{2}}}\left(2\,-\,3\frac{R^2-d^2}{\left(R^2+\frac{d^2}{4}\right)^2}z^2\right)
En faisant d = R :
\Large \left(B_1+B_2\right)_{z=0}\,=\,\frac{\mu_0NIR^2}{2} \left[\frac{2}{ \left(R^2+\frac{R^2}{4}\right) ^{\frac{3}{2}}}\,-\,3\frac{R^2-R^2}{\left(R^2+\frac{R^2}{4}\right) ^{\frac{7}{2}}}\right]

\Large \boxed{\left(B_1+B_2\right)_{z=0}\,=\,\left(\frac{4}{5}\right)^{\frac{3}{2}}\,\frac{\mu_0NI}{R}}
Formule qui avait été évoquée précédemment mais sans démonstration...

On fait de même pour l'autre cas
\Large \left(B_1-B_2\right)_{z=0}\,=\,K\left[R^2+\frac{d^2}{4}\right]^{-\frac{3}{2}}\,+\,z\,\,3K\frac{d}{2}\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\,+\,\frac{z^2}{2}\,\,3K\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\left[5\frac{d^2}{4}\left[R^2+\frac{d^2}{4}\right]^{-1}-1\right]\\ -\,K\,\left[R^2+\frac{d^2}{4}\right]^{-\frac{3}{2}}\,+\,\,z\,\,3K\frac{d}{2}\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\,-\,\frac{z^2}{2}\,3K\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\left[5\frac{d^2}{4}\left[R^2+\frac{d^2}{4}\right]^{-1}-1\right]
\Large \left(B_1-B_2\right)_{z=0}\,=\,3Kd\left[R^2+\frac{d^2}{4}\right]^{-\frac{5}{2}}\,z
Si d = R :
\Large \left(B_1-B_2\right)_{z=0}\,=\,3\,\frac{\mu_0NIR^2}{2}\,R\,\left[R^2+\frac{R^2}{4}\right]^{-\frac{5}{2}}\,z
\Large \left(B_1-B_2\right)_{z=0}\,=\,3\,\frac{\mu_0NIR^3}{2}\,\left[R^2+\frac{R^2}{4}\right]^{-\frac{5}{2}}\,z
\Large \boxed{\left(B_1-B_2\right)_{z=0}\,=\,3\left(\frac{\,4\,}{\,5\,}\right)^{\frac{5}{2}}\frac{\mu_0NI}{2R^2}\,z}

On trouve donc le champ magnétique proportionnel à z (conformément aux réponses proposées dans le QCM).

Tous les calculs sont à refaire et à vérifier, bien entendu...

Posté par
lounastrere : Induction de bobines sur l'axe 19-03-13 à 21:33

Merci beaucoup aragorn !  

Sincèrement, t'es un champion!

Mais le seul petit problème, c'est qu'en passant à l'application numérique je trouve 12,95.10^-4 T,qui ne correspond à aucune proposition de l'énoncé ...

Voudrais-tu bien m'accompagner encore seulement un peu au bout de ce long chemin périlleux ?

Merci beaucoup !

Posté par
lounastrere : Induction de bobines sur l'axe 19-03-13 à 21:35

Je voulais dire 12,95.10^-4 z T, évidemment ...

Posté par
Aragornre : Induction de bobines sur l'axe 19-03-13 à 21:37

Oui mais il me manque le nombre de spires N

Posté par
lounastrere : Induction de bobines sur l'axe 19-03-13 à 21:50

En fait il me semble qu'il est implicite que le nombre de spires est 1 d'après l'énoncé ...

Posté par
Aragornre : Induction de bobines sur l'axe 19-03-13 à 22:46

Citation :
Deux bobines circulaires d'axe Oz  et de rayon R=5 cm sont placées l'une en face de l'autre sur l'axe Oz a une distance R l'une de l'autre, de part et d'autre de l'origine O .

En général, une "bobine" est constituée de plusieurs spires sinon on écrit : "deux spires circulaires"... enfin, à mon avis...
Mais, bon, 1 spire, je veux bien...

Posté par
Aragornre : Induction de bobines sur l'axe 19-03-13 à 22:50

Il ne faut pas oublier que, dans la question 2 du QCM, il est précisé que z est en cm, pas en m...
12,95.10-4 z T, ce n'est pas tellement loin de 12,95 µT ou 12,95 mT

Posté par
Aragornre : Induction de bobines sur l'axe 19-03-13 à 22:54

Dans la réponse que j'ai écrite, z est en m...
les réponses signifient que :
1) dans le 1er cas, le champ magnétique est constant autour de l'origine (tant que le développement limité est valide)
2) dans le 2ème cas, le champ magnétique change de sens en O et s'annule en O. Il est proportionnel à z autour de l'origine (tant que le développement limité est valide)

Posté par
lounastrere : Induction de bobines sur l'axe 19-03-13 à 23:07

D'accord, donc, déjà, si ton z est en mètres, alors je dois aussi prendre R en mètres, c'est ca, puis multiplier par 100 pour avoir des centimètres ...

J'aurais juste une petite question : si par rapport à la question 1 les champs sont en sens inverse, la résultante au voisinage de O n'est-elle pas sensée etre inférieure à la réponse de la question 1 ?

Merci d'avance

Posté par
Aragornre : Induction de bobines sur l'axe 20-03-13 à 11:13

Il n'y a que z qui est en cm... Je sais, ce n'est pas habituel mais c'est un piège...
Donc R est en m parce qu'il fait partie de la constante qui est devant z. Bien entendu, normalement z est en m (unité du système SI).
\Large \boxed{\left(B_1-B_2\right)_{z=0}\,=\,3\left(\frac{\,4\,}{\,5\,}\right)^{\frac{5}{2}}\frac{\mu_0NI}{2R^2}\,z}

\Large \left(B_1-B_2\right)_{z=0}\,=\,3\left(\frac{\,4\,}{\,5\,}\right)^{\frac{5}{2}}\frac{4\pi.10^{-7}\,.\,3}{2\,.\,(5.10^{-2})^2}\,z\,=\,1,295.10^{-3}\,z\,\,\,\,T   avec z en m
Maintenant, étudions de plus près cette histoire de "z en cm"...
Si z = 1 m, on peut l'écrire z = 100 cm 10-2
Autrement dit, \Large z_m\,=\,10^{-2}\,z_{cm}
en reportant cela dans la formule
\Large \left(B_1-B_2\right)_{z=0}\,=\,3\left(\frac{\,4\,}{\,5\,}\right)^{\frac{5}{2}}\frac{\mu_0NI}{2R^2}\,z_m\,\Rightarrow\,\left(B_1-B_2\right)_{z=0}\,=\,3\left(\frac{\,4\,}{\,5\,}\right)^{\frac{5}{2}}\frac{\mu_0NI}{2R^2}\,10^{-2}\,\,z_{cm}\,=\,1,295.10^{-3}\,.\,10^{-2}\,\,z_{cm}\,\,\,\,T
D'où :
\Large \left(B_1-B_2\right)_{z=0}\,=\,12,95.10^{-6}\,\,\,z_{cm}\,\,\,\,T
Donc :
\Large \left(B_1-B_2\right)_{z=0}\,=\,12,95\,\,\,z_{cm}\,\,\,\,\mu T

Citation :
si par rapport à la question 1 les champs sont en sens inverse, la résultante au voisinage de O n'est-elle pas sensée etre inférieure à la réponse de la question 1 ?

Eh bien, je pense que c'est le cas... Dans la 1ère question , on trouve 53,95 µT et dans la 2ème, 12,95 zcm µT. Il faut être à 4,16 cm pour que le champ de la 2ème question soit égal au champ de la 1ère en Z = 0. Comme les bobines (ou plutôt les spires ) sont à 2,5 cm de chaque côté de l'origine...

Posté par
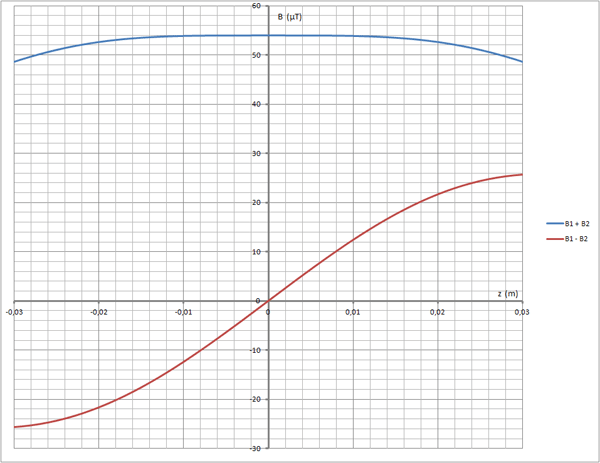
Aragornre : Induction de bobines sur l'axe 20-03-13 à 11:58

Pour avoir une idée du résultat, on peut faire un graphique (à partir des formules d'origine et non pas à partir des développements limités).
On voit effectivement que B1 + B2 est constant jusqu'à \pm\, 1\,cm  de l'origine au moins (tant que le développement limité est valide). Et B1 - B2 s'annule à l'origine et change de sens à l'origine. De plus, la courbe B1 - B2 est une droite (B1 - B2 proportionnel à z) jusqu'à \pm\, 1\,cm  de l'origine au moins (tant que le développement limité est valide).  

Induction de bobines sur l\'axe

Posté par
lounastrere : Induction de bobines sur l'axe 21-03-13 à 09:10

Waouh ! Vraiment Aragorn, tu es super !

Merci pour toutes ces explications si claires et ce graphe qui illustre parfaitement ton propos et qui m'en montre meme plus que ce que j'espèrais

Un grand merci pour ta patience !

A bientot !

Posté par
Aragornre : Induction de bobines sur l'axe 21-03-13 à 10:36

Je me suis bien amusé avec cet exercice...
A bientôt !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !