Inscription / Connexion Nouveau Sujet
Induction
Bonsoir,
J'ai quelques questions concernant le chapitre sur l'induction, merci de vos réponses.
1. Dans quels cas peut-on négliger les phénomènes d'auto-induction ?
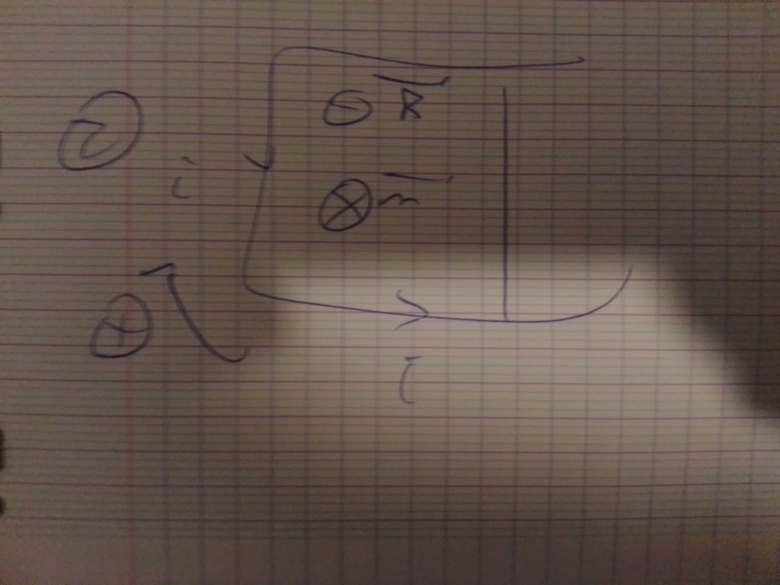
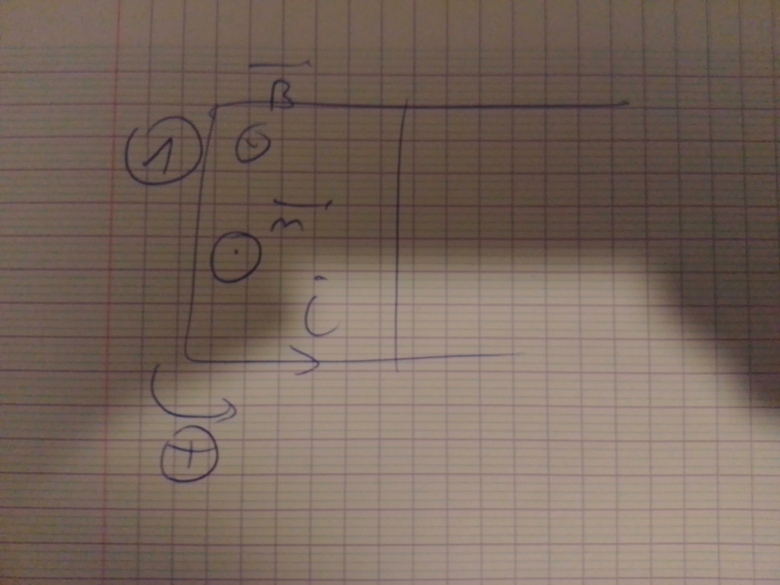
2. Dans l'exemples des rails de Laplace, on a dit qu'on orienté arbitrairement puis qu'on donnait un sens de parcours de la normale identique au sens pour le courant. Néanmoins, peut-on faire le choix de les orienter dans des sens différents, voir schéma joints, ci oui, aboutit-t-on au même résultat à la fin ?
De façon plus générale, la pour (règle du tire-bouchon) se fait-elle indépendamment de celle pour la normale, ou la normale est-elle fixée par le sens du courant ?
Bonjour,
1- On néglige les les phénomènes d'auto-induction quand le flux du champ magnétique peut être considéré comme le flux du champ extérieur. Autrement dit, il faut que le champ magnétique créé par le courant soit négligeable par rapport au champ extérieur.
2- Les deux conventions sont liées pour donner e=Ri. SI vous ne liez pas les deux conventions, vous pourriez avoir e=Ri ou e=-Ri. Dit autrement, dans , le vecteur surface est orienté par la règle du tire-bouchon à partir de i. Remarque :
est une donnée.
La règle que vous avez énoncé s'applique t-elle aussi pour la définition de l'intensité en fonction de \( \overrightarrow{j} \), où dans ce cas-là, peut-on choisir la normale comme on le veut.
Ce n'est pas le même problème.
Dans le cas de e=Ri, on utilise le théorème de Stockes et le sens de la circulation impose le sens du vecteur surface du flux.
Dans le cas de la définition du courant, on ne peut définir une circulation sur le pourtour du fil ; par contre le sens du vecteur surface donne bien le sens de i.
Vous voulez donc dire qu'on fixe arbitrairement la circulation pour le fil est que en fonction de la convention choisie, on déduit la direction du vecteur surface.
Ensuite, une dernière question, dans notre cours on a écrit la relation de passage pour le champ magnétique, à savoir dans le cas de la couche plane. Néanmoins, peut-on utiliser cette relation dès que l'on en présence d'une surface délimitant deux milieux différents ?
On fixe arbitrairement la circulation pour le fil et, en fonction de la convention choisie, on en déduit la direction du vecteur surface.
C'est bien cela.


