Inscription / Connexion Nouveau Sujet
Indication balance
Bonjour,
Expliquer le résultat obtenu par les balances.
Cas 1: Nous pesons une bille en plomb, la balance indique une masse m1.
Cas 2: Nous pesons une bille en bois, la balance indique une masse m2.
Cas 3: Nous pesons un bécher rempli d'eau, la balance indique une masse m3.
Cas 4: Nous pesons un bécher rempli d'eau avec une bille en plomb (la bille coule), la balance indique une masse m4.
Cas 5: Nous pesons un bécher rempli d'eau avec une bille en bois (la moitié du volume de la bille en bois se trouve dans l'air, l'autre moitiée dans l'eau), la balance indique une masse m5.
Cas 6: Nous pesons un bécher rempli d'eau avec une bille en plomb au centre du bécher tenu par un fil relié à une potence qui est sur une table à côté de la balance, la balance indique une masse m6.
Je pense que la balance mesure la force qui est exercée par le système au-dessus de la balance sur la balance puis la convertie en masse en divisant la force par l'intensité de pesanteur g. Nous ne prenons pas en compte les forces de pressions du fait de la 3ème loi de Newton sur l'action/réaction, la force de pression exercée sur certaines particules d'air a sa réciproque, donc les 2 forces s'annulent 2 à 2 et on peut généraliser ce principe sur tout l'air au-dessus de la balance.
Dans tout les cas que je vais considéré, le référentiel sera le référentiel terrestre considéré comme galiléen:
Cas 1: système: bille en plomb
On applique le principe fondamental de la statique sur notre système: P(bille en métal) = Rn1 avec P1 le poids de la bille en plomb et Rn1 la réaction normale de la balance sur la bille en plomb.
Cette réaction sera toujours présente, c'est cette valeur qui permet d'indiquer la masse de la bille en plomb.
Masse indiquée par la balance: m1 qui correspond à la masse de la bille en plomb
Cas 2: Même raisonnement
Masse indiquée par la balance: m2 qui correspond à la masse de la bille en bois
Cas 3: Même raisonnement
Masse indiquée par la balance: m3 qui correspond à la masse du système bécher+eau
Cas 4: j'applique le principe fondamental de la statique sur le système bécher+eau+bille en plomb
Rn4=P(becher+eau+bille en plomb)-A(poussée d'Archimède)
Donc la balance indique la masse m4 qui correspond à la masse du système (bécher+eau+bille en plomb) -  eau*Vimergé de la bille en plomb
eau*Vimergé de la bille en plomb
Cas 5: Même raisonnement
La balance indique la masse m5 qui correspond à la masse du système (bécher+eau+bille en bois) -  eau*Vimergé de la bille en bois
eau*Vimergé de la bille en bois
Cas 6: j'applique le principe fondamental de la statique sur le système bille en plomb, j'obtiens que T=P(bille en plomb) -A
J'applique le principe fondamental de la statique sur le système bécher+eau+bille en plomb.
J'obtiens Rn6= P(becher+eau) + P(bille en plomb) - A - T
Or T=P(bille en plomb)-A
Donc, Rn6=P(bécher +eau)
La balance indique une masse m6 qui correspond à la masse du système (bécher+eau)
Qu'en pensez-vous ?
Bonsoir
Pas de difficulté bien sûr pour les trois premier cas. Ensuite, comme tu l'as dit, il faut appliquer le plus astucieusement possible le principe des actions réciproques, sachant que la poussée d'Archimède est une force de pression exercée par un solide sur un liquide. Le solide exerce donc ici une force opposé à la poussée d'Archimède.
Ceci étant posé, l'indication de la balance est égale à la force (au facteur g près) exercée par le plateau de la balance sur l'ensemble {bécher - eau} pour maintenir ce système {bécher-eau} en équilibre.
Si j'ai bien compris, pour les cas 4,5 et 6, la balance indique juste la masse du système {bécher+eau} ?
Pas si simple !
Dans le cas 4 : la bille en plomb exerce une force sur le fond du bécher. La balance va certainement indiquer une valeur supérieure à m3 !
Réfléchis bien à ce que j'ai écris sur la poussée d'Archimède et le principe des actions réciproques.
D'accord,
Pour le cas 4: j'étudie le système {bécher+eau+bille}
Bilan des forces extérieures appliquées à ce système: le poids de l'eau, le poids du bécher, le poids de la bille, la poussée d'Archimède A et la réaction normale du plateau de la balance Rn4.
En appliquant le principe fondamental we la statique et en le projettant sur l'axe vertical, j'obtiens: Rn4=Psystème-A
La balance indique donc Rn4/g
Mais en relisant l'aide apportée, j'hésite à dire que la poussée d'Archimède est une force extérieure au système car il y a la réaction du fluide sur la bille.
Alors Rn4=masse(eau+bécher+bille)
Cas 5:
Système: bille+bécher+eau
Bilan des forces: Poids système, Réaction normale Rn5, poussée d'Archimède
Ici, on prend en compte la poussée d'Archimède car il n'y a pas la force de réaction dans le système, en effet il s'agit de la force de pression liée à l'air
Alors, Rn5=Psystème-A
Cas 6: Même raisonnement que cas 4:
Rn6=Peau+bécher+bille
4 : seul le deuxième raisonnement est correct.
5 : Ok
6 : non. Tu oublies le rôle du fil... tu as intérêt à étudier l'équilibre de l'ensemble (eau-becher ).
Cas 6:
J'étudie le système {bécher+eau+bille}
Les forces extérieures appliquées à ce système sont: le poids du système, la force de tension du fil.
J'applique le principe fondamental de la statique et je le projette sur l'axe vertical:
Rn6=Psystème-T
Déterminons T:
J'etudie le système de la bille
J'applique le principe fondamental de la statique à ce système et je le projette sur l'axe vertical: P=A+T donc T=P-A
Donc Rn6=Psystème -(P-A)
Rn6=Peau+bécher+A
Résultat correct qui aurait pu être obtenu de façon immédiate en appliquant le principe des actions réciproques.
Effectivement : l'application du principe des actions réciproques ne parait pas toujours intuitive. Je l'ai constaté maintes fois...La situation est pourtant simple...
On part de la situation du bécher rempli en partie d'eau (indication m3 de la balance) : par rapport à cette situation, l'eau se trouve soumise à une force supplémentaire : l'action du solide sur l'eau. Selon le principe des actions réciproques, cette action est tout simplement l'opposé de la poussée d'Archimède :
m6=m3+ eau.Vsolide
eau.Vsolide
Puisque : m1= solide.Vsolide , tu as ici le principe d'une méthode très précise de mesure de la densité par rapport à l'eau d'un solide de forme quelconque :
solide.Vsolide , tu as ici le principe d'une méthode très précise de mesure de la densité par rapport à l'eau d'un solide de forme quelconque :
Bonsoir,
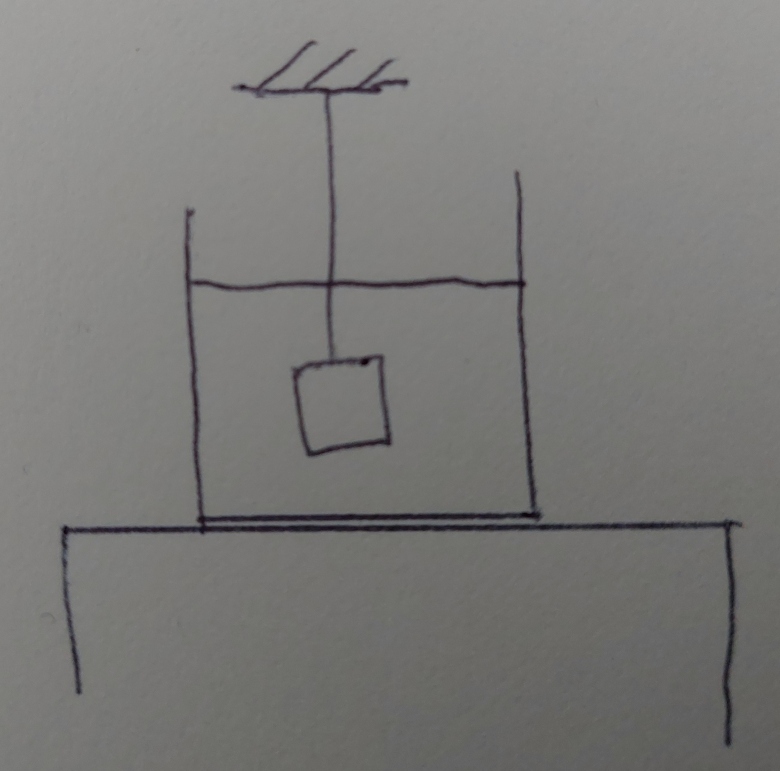
Je souhaite déterminer la poussée d'Archimède. J'ai ce système, cf schéma.
J'applique le principe fondamental de la statique sur la masse:
Bilan des forces extérieures s'appliquant sur la masse:
A: poussée d'Archimède, verticale ascendante
T: tension du fil, verticale ascendante
Pm: poids de la masse, verticale descendante
j'obtiens en projetant sur l'axe vertical ascendant:
A = Pm - T
Le poids je peux le mesuré mais la tension non alors c'est une inconnue.
Détermination de T:
J'applique le principe fondamental de la statique sur le système : masse, bécher, eau:
Les forces extérieures agissant sur le système:
P(b+e) : poids bécher+eau, verticale descendante
Pm: poids masse, verticale descendante
T: tension du fil, verticale ascendante
R: réaction de la balance sur le bécher, verticale ascendante
En projetant sur l'axe vertical ascendant:
T = R - Pm - P(b+e)
Je remplace donc cette expression de T dans l'expression de la poussée d'Archimède:
A = P(b+e) - R
Cependant, le professeur m'a indiqué que ça ne fonctionne pas car la force de tension n'intervient pas dans le deuxième cas car elle agit sur un sous-système de mon système et en déterminant la poussée d'Archimède ainsi, c'est le serpent qui se mord la queue.
Qu'en pensez-vous ?
Si une force extérieure agit sur un sous-système du système, agit-elle de facto sur le système ?
Merci d'avance
Si une force extérieure agit sur un sous-système du système, agit-elle de facto sur le système ?
La réponse à cette question est a priori oui mais ce n'est peut-être pas exactement ce que veut dire, un peu maladroitement, ton professeur. Quelques précisions...
1° on ne peut définir correctement une force qu'en précisant :
1° : par quoi est elle exercée ;
2° : sur quoi elle est exercée .
Sans ces deux précisions, aucun raisonnement rigoureux n'est passible.
2° l'équilibre d'un système prend en compte toutes les forces extérieures c'est à dire toutes les forces exercées par le milieu extérieur sur tout ou partie du système étudié.
3° pour en revenir à l'argumentation de ton professeur : si une force est exercée sur un sous-système du système à l'équilibre par le milieu extérieur, il faut la prendre en compte ; si une force est exercée sur un sous-système du système à l'équilibre par un autre sous-système du système à l'équilibre, cette force est une force intérieure qui n'intervient pas directement dans l'application des théorèmes généraux de la statique.
J'ai répondu hier soir à la question précise sur la notion de force extérieure.
Je réponds maintenant à propos de ton raisonnement sur la poussée d'Archimède. Tu as déjà fait ce raisonnement dans ton message du 21-10-21 à 22:32. Ici, tu as commis une erreur de signe en projetant la condition d'équilibre du système {masse, bécher,eau}. Il aurait fallu écrire :
T+R-P(b+e)-Pm=0
Tu obtiens alors le même résultat que dans ton message du 21-10-21 à 22:32 :
A=R-P(b+e)
La justification de l'inégalité : R > P(b+e) t'a été fournie dans mon message du 21-10-21 à 23:38 faisant intervenir le principe des actions réciproques.
Merci pour cette clarté.
Effectivement, je n'ai pas considérer la corde comme étant dans mon système (ni sous-système) de ce fait, la force de tension exercée par cette corde sur la masse est une force extérieure.
Cette méthode me parait valable pour mesurer la poussée d'Archimède. Si je tare la balance lorsqu'il y a le bécher remplit d'eau, la valeur indiqué par la balance représente l'équivalent massique de la poussée d'Archimède. Je peux mettre un support élevateur sous la balance pour observer qualitativement et quantitativement la valeur de la poussée d'Archimède en fonction du volume de la masse immergé ainsi que ses caractéristiques. Et la qualitativement, la différence de valeur entre la poussée d'Archimède lorsque l'air est le fluide et lorsque c'est l'eau.
Qu'en pensez-vous ?
Le professeur avait une autre idée en tête, il nous a proposé la même expérience sans balance mais avec un dynamomètre à la place.
Si j'ai bien compris le dynamomètre mesure l'intensité des forces extérieures qui s'applique sur lui.
Donc si j'appelle T la valeur de la tension du dynamomètre:
J'applique le principe fondamental de la statique sur la masse:
Pm+A+T=0
En projettant sur l'axe vertical ascendant j'obtiens:
T = Pm - A (valeur lu)
Donc si à l'état initial, la masse est dans l'air et je le plonge petit à petit en notant le volume et la valeur sur la dynamomètre,. La valeur de T devrait baisser. Lorsque j'ai fait l'expérience, je trouvais que les variations de T était assez faible donc difficilement mesurable et pas très précis. Pour améliorer la précision, je dirais de prendre une éprouvette graduée plus étroite et un dynamomètre ayant une plus petite plage de validité et donc plus de graduation.
Qu'en pensez-vous ?
Connaissez-vous d'autres méthodes relativement faciles expérimentalement pour avoir ces mesures ?
La méthode la plus précise est celle qui vient d'être détaillée dans les messages précédents. En effet, on sait actuellement fabriquer des balances électroniques extrêmement précises et fiables pour des prix raisonnables.
On peut aussi utiliser un dynamomètre : dans l'air, il indique le poids P de l'objet suspendu (on suppose un objet dense de façon à pouvoir négliger la poussée d'Archimède due à l'air). Quand l'objet est suspendu au dynamomètre tout en étant immergée dans le liquide, il indique (P-A) . Par différence entre les deux mesures, on obtient A. Cette méthode est cependant moins bonne :
1° : erreur systématique due à la poussée d'Archimède exercée par l'air ;
2° : les dynamomètres sont nettement moins sensibles et surtout moins fidèles que les balances électroniques modernes mais le prix n'est pas le même...


