Niveau licence

Incertitude Optique

Posté par
Norticus666 08-03-09 à 13:24

Bonjour à vous, oui vous qui lisez ces lignes !!

Alors voila je suis completement dépassé au niveau des incertitudes et il se trouve que j'ai un exo dessus... Voila j'expose le probleme

Nom de l'exo: Focometrie des lentilles minces
A partir de l'expression littérale de f' pour chaque méthode, établir l'expression de l'incertitude absolue f'.

Méthode de la relation de conjugaison:
1/SA' - 1/SA = 1/f'
soit Grand transv= SA'/SA

Méthode de Bessel:
f'= (D² -d ²)/4D
Avec:
D la distance entre l'objet et l'écran
d la distance positive entre les deux positions de la lentille

Schema si besoin:

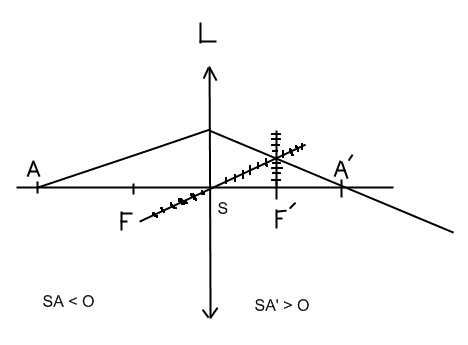
Incertitude Optique

Posté par re : Incertitude Optique 08-03-09 à 20:12

Bonsoir,
A mon avis, c'est :
$\frac{\Delta f^'}{f^'}\,=\,2\,\frac{\Delta D}{D}\,+\,2\,\frac{\Delta d}{d}\,+\,4\,\frac{\Delta D}{D}$
Donc, a priori : $\frac{\Delta f^'}{f^'}\,=\,6\,\frac{\Delta D}{D}\,+\,2\,\frac{\Delta d}{d}$

sauf erreur de ma part...

Posté par re : Incertitude Optique 08-03-09 à 20:23

non, je me suis trompé...
$\frac{\Delta f^'}{f^'}\,=\,2\,\frac{\Delta D}{D^2-d^2}\,+\,2\,\frac{\Delta d}{D^2-d^2}\,+\,\frac{\Delta D}{D}$

Posté par re : Incertitude Optique 09-03-09 à 09:06

J'en ai perdu en route ... La formule n'est pas homogène...
$\frac{\Delta f^'}{f^'}\,=\,\frac{2\,D}{D^2-d^2}\,\Delta D\,+\,\frac{2\,d}{D^2-d^2}\,\Delta d\,+\,\frac{\Delta D}{D}$

Posté par re : Incertitude Optique 09-03-09 à 11:17

Daccord mais j'avais une question assez bete mais que je trouve importante:
Comment avez vous fait?
Car c'est pas tout de recopier ceci mais pour moi même j'aimerais comprendre histoire de me coucher moin bète en ces jours de blocage.

Posté par re : Incertitude Optique 09-03-09 à 11:21

Et j'allais oublier, pour la Méthode de la relation de conjugaison:
1/SA' - 1/SA = 1/f'

Sa ce passe comment?

Posté par re : Incertitude Optique 09-03-09 à 18:07

Cela s'étudie en 1ère année de fac, sauf erreur de ma part...
Je vais prendre un exemple plus simple que celui-là.
Le principe, c'est de prendre la différentielle.
Je prends $P\,=\,\frac{U^2}{R}$
$\delta P\,=\,\Big(\frac{U^2}{R}\Big)^'\delta U\,+\,\Big(\frac{U^2}{R}\Big)^'\delta R$
$\delta P\,=\,\Big(\frac{2U}{R}\Big)\delta U\,-\,\Big(\frac{U^2}{R^2}\Big)\delta R$

Là, on peut transformer les différentielles en incertitudes
$\Delta P\,=\,\Big(\frac{2U}{R}\Big)\Delta U\,+\,\Big(\frac{U^2}{R^2}\Big)\Delta R$

Mais on peut transformer cela en incertitude relative
$\frac{\Delta P}{P}\,=\,\frac{R}{U^2}\,\Big(\frac{2U}{R}\Big)\Delta U\,+\,\frac{R}{U^2}\,\Big(\frac{U^2}{R^2}\Big)\Delta R$
$\frac{\Delta P}{P}\,=\,2\,\frac{\Delta U}{U}\,+\,\frac{\Delta R}{R}$

J'ai appris encore une autre façon...
On prend le Ln des 2 membres.
Ln(P) = Ln(U²) - Ln(R)
$Ln(P)\,=\,2\,Ln(U)\,-\,Ln(R)$
Et on prend la dérivée :
$\frac{dP}{P}\,=\,2\,\frac{dU}{U}\,-\,\frac{dR}{R}$
Et on transforme en incertitudes relatives :
$\frac{\Delta P}{P}\,=\,2\,\frac{\Delta U}{U}\,+\,\frac{\Delta R}{R}$

On peut généraliser en disant :
1) l'incertitude absolue d'une somme (ou d'une différence) est égale à la somme des incertitudes relatives
f = a + b ==> f = a + b
2) l'incertitude relative d'un produit ou d'un quotient est égale à la somme des incertitudes relatives
f = ab ou f = a/b
$\frac{\Delta f}{f}\,=\,\frac{a^'}{a}\,\Delta a\,+\,\frac{b^'}{b}\,\Delta b$

La méthode en vogue actuellement semble être la différentielle.

On peut appliquer la méthode au cas qui nous intéresse mais j'ai l'impression qu'on ne trouve pas ce que j'ai mis précédemment...
Je refais les calculs...

Posté par re : Incertitude Optique 09-03-09 à 19:46

On a donc $f^'\,=\,\frac{D^2-d^2}{4D}$
Donc :
$\delta f^'\,=\,\Big(\frac{D^2-d^2}{4D}\Big)^'\delta D\,+\,\Big(\frac{D^2-d^2}{4D}\Big)^'\delta d$
que je pourrais écrire aussi :
$\delta f^'\,=\,\frac{d}{dD}\Big(\frac{D^2-d^2}{4D}\Big)\,\delta D\,+\,\frac{d}{dd}\Big(\frac{D^2-d^2}{4D}\Big)\,\delta d$
$\delta f^'\,=\,\frac{8D^2-4D^2+4d^2}{16D^2}\delta D\,+\,\frac{-2d}{4D}\,\delta d$
$\delta f^'\,=\,\frac{D^2+d^2}{4D^2}\delta D\,-\,\frac{2d}{4D}\,\delta d$
On peut donc en déduire directement l'incertitude absolue $\Delta f^'$
$\Delta f^'\,=\,\frac{D^2+d^2}{4D^2}\Delta D\,+\,\frac{2d}{4D}\,\Delta d$

Et je pense que c'est la bonne réponse... sauf erreur de ma part...

Pour 1/SA' - 1/SA = 1/f', je pense qu'il faut l'écrire sous la forme :
$\frac{1}{f^'}\,=\,\frac{1}{\bar{SA'}}\,-\,\frac{1}{\bar{SA}}$
$f^'\,=\,\frac{\bar{SA}\,\bar{SA'}}{\bar{SA}-\bar{SA'}}$
Pour appliquer la méthode de la différentielle, il est plus pratique (peut-être ! ) de poser $\bar{SA}\,=\,x$ et $\bar{SA'}\,=\,y$ , par exemple.
$f^'\,=\,\frac{x\,y}{x-y}$
$\delta f^'\,=\,\frac{d}{dx}\Big(\frac{x\,y}{x-y}\Big)\delta x\,+\,\frac{d}{dy}\Big(\frac{x\,y}{x-y}\Big)\delta y$