Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Impédance complexe et intensité complexe

Posté par
Tirlititi 24-03-16 à 17:58

Bonjour,

J'ai mis ci-dessous le sujet.
J'ai du mal à voir bien clair la fin de la question 8.
Je vous mets ce que j'ai trouvé pour l'instant :

Q6
p_g = v_g * i = 2 V_g * I * cos(wt) * cos(wt-phi)
p_g = = 2 V_g * I * cos(wt) * (cos(wt)cos(phi) - sin(wt)sin(phi))

Q7
P_g = < p_g > = 2 V_g * I * cos(phi) / 2 = V_g * I * cos(phi) (en utilisant le fait que valeur moyenne de sin*cos = 0)

Q8
P = R*I^2
Zt = Z + Zg = (R+R_g) + j(X+X_g)
V_g = Z_t*I ..........donc.......... I = V_g/Z_t

En fait je vois mal comment exprimer la puissance moyenne de tout un circuit. Pourtant je n'ai pas trouvé dur de calculer la puissance du générateur uniquement.

Je vous remercie par avance pour votre aide.

Posté par
Tirlititire : Impédance complexe et intensité complexe 24-03-16 à 17:59

Ci joint le sujet, je suis désolé de l'oubli

Posté par
Tirlititire : Impédance complexe et intensité complexe 24-03-16 à 18:00

J'ai l'impression que mon image ne passe pas et je n'arrive pas à éditer.
Je m'excuse !

Posté par
Tirlititire : Impédance complexe et intensité complexe 24-03-16 à 18:05

Si un modérateur passe par là il peut supprimer les messages inutiles, toutes mes excuses.
Si quelqu'un sait pourquoi mon image ne passe pas ou comment supprimer ca me ferait plaisir aussi.

Je vous écris les questions :

vg = Vg * sqrt(2) * cos(wt)
i = I * sqrt(2) * cos(wt-phi)
Zg = Rg + j Xg et Z = R + jX


Q6) Exprimer la puissance pg fournie par la source de tension alternative parfaite vg, en fonction de Vg, I, phi et wt.

Q7) Exprimer la valeur moyenne Pg de la puissance instantanée pg, exprimée à la question Q6 en fonction de Vg, I et phi

Posté par
Tirlititire : Impédance complexe et intensité complexe 24-03-16 à 18:24

Je crois que j'ai compris ce qui clochait. Je m'excuse pour la gêne occasionnée.
Si quelqu'un veut bien m'aider, voici l'image.

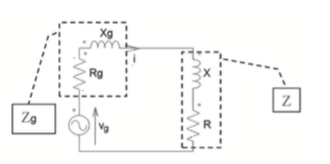
Impédance complexe et intensité complexe

Posté par
vanoisere : Impédance complexe et intensité complexe 24-03-16 à 20:58

Bonsoir, je réponds juste à Q8, le reste est une application directe du cours.
Tu vas obtenir :

P=R\cdot I^{2}=\frac{R}{\left(R+R_{g}\right)^{2}+\left(X+X_{g}\right)^{2}}\cdot V_{g}^{2}
Ensuite , tu calcules les dérivées partielles de P par rapport à X puis par rapport à P, afin d'étudier les influences de X et R sur P, les autres grandeurs étant fixes.
Tu devrais arriver à la conclusion que la puissance est maximale si X = -Xg et si R = Rg , ce qui peut se résumer en disant que l'impédance complexe du récepteur doit être égale au conjugué de l'impédance complexe du générateur pour que la puissance transmise soit maximale. Dans ce cas particulier, il y a "adaptation d'impédance".

Posté par
vanoisere : Impédance complexe et intensité complexe 24-03-16 à 21:01

Citation :
Ensuite , tu calcules les dérivées partielles de P par rapport à X puis par rapport à R

Excuse la faute de frappe...

Posté par
Tirlititire : Impédance complexe et intensité complexe 24-03-16 à 22:03

Merci pour votre réponse ! je pense que j'ai compris

Je ne vous demande pas un rédigé des Q6 et Q7 comme vous l'avez fait pour la Q8 mais j'ai écrit mes réponses et je suis quasi sûr que c'est correct, ce serait juste possible de me le confirmer ?

Posté par
Tirlititire : Impédance complexe et intensité complexe 24-03-16 à 22:08

Ah oui et j'ai une autre question, vous écrivez :

vanoise @ 24-03-2016 à 20:58


P=R\cdot I^{2}=\frac{R}{\left(R+R_{g}\right)^{2}+\left(X+X_{g}\right)^{2}}\cdot V_{g}^{2}


Or Zt est complexe, donc I est complexe, je noterai I de cette manière :

I = \frac{V_g}{(R+R_g)+j(X+X_g)}

Et en mettant I au carré si le I que j'ai mi ci-dessus est juste vous prenez le module au carré, c'est toujours le module que l'on prend ?

Posté par
vanoisere : Impédance complexe et intensité complexe 24-03-16 à 22:49

Il me semble que le carré du module d'un complexe est égal au produit du complexe par son conjugué... Vive les maths !

Posté par
Tirlititire : Impédance complexe et intensité complexe 24-03-16 à 23:49

oui du coup on prend bien le module.
on aurait pu faire complexe*complexe dans ma tête mais enfin je retiens.

et q6 et q7 ?

Posté par
vanoisere : Impédance complexe et intensité complexe 25-03-16 à 00:23

Q6 : tu aurais pu aller plus vite en transformant ton produit de cosinus en une somme de deux termes : un terme constant faisant intervenir cos() et un terme faisant intervenir un cosinus dont la valeur moyenne sur une période est nulle. Cette méthode de fournit sans calcul supplémentaire la réponse q7. Cela dit : ce que tu as fait est correct.

Posté par
vanoisere : Impédance complexe et intensité complexe 25-03-16 à 13:45

Bonjour,
En complément à mon message précédent :

\cos\left(a\right)\cdot\cos\left(b\right)=\frac{1}{2}\left[\cos\left(a-b\right)+\cos\left(a+b\right)\right]
Appliqué au contexte :

\\ p_{g}(t)=2\cdot V_{g}\cdot I\cdot\cos\left(\omega t+\varphi\right)\cdot\cos\left(\omega t\right)=V_{g}\cdot I\cdot\cos\left(\varphi\right)+V_{g}\cdot I\cdot\cos\left(2\omega t+\varphi\right)
La valeur moyenne sur une période de \cos\left(2\omega t+\varphi\right)   étant nulle, on obtient directement la puissance moyenne sur une période ou un multiple de la période :

\\ P_{g}=V_{g}\cdot I\cdot\cos\left(\varphi\right)


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !