La première expression résulte de la loi d'Ohm.
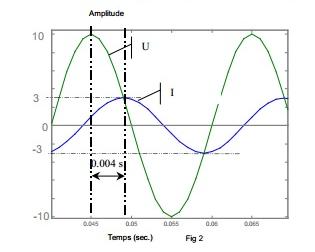
Dans la deuxième expression, ce que tu as appelé " déphasage " est en réalité l'écart de temps qui sépare les maxima des courbes U et I. Cette expression traduit le fait que le rapport de l'angle de déphasage à l'angle  2 radians est égal à celui de cet écart de temps à la période des sinusoides.

Quand je parlais de la première formule, j'entendais celle de l'impédance complexe. Pourquoi ? Comment peut-on trouver cette expression de l'impédance complexe ?

Et je suis désolée, mais je n'ai pas très bien compris votre explication, visuellement sur le dessin concernant la dernière formule

Les angles de phase de la tension u(t) et du courant i(t) étant respectivement _u et _i , l'argument de l'impédance complexe est égal à la différence de phase = _u et _i entre la tension et l'intensité dont l'impédance est le siège. Cette différence de phase peut être calculée en fonction du décalage temporel entre les courbes représentant u(t) et i(t).                          

Votre explication est assez claire. Cependant, que voulez-vous dire par "dont l'impédance est le siège" ? Que représente l'argument de l'impédance sur le dessin des courbe? est-il représentable? Et pourquoi "2pi" * dephasage/période ?

Cette formule peut-elle être apprise et replacer dans le cas dans les cas similaire ? Ou doit-elle être comprise et adaptée à chaque fois?

merci beaucoup d'avance

" dont l'impédance est le siège " : je veux dire simplement que l'impédance a, à ses bornes, la tension u(t) et qu'elle est parcourue par le courant i(t).
L'argument de l'impédance ne se voit pas directement sur les dessins. Mais il peut être aisément déduit de l'écart temporel qui apparaît entre les courbes (celles-ci sont telles qu'on pourrait les observer sur l'écran d'un oscilloscope à deux voies, l'une recevant u(t) et l'autre i(t) ).
Si t est l'écart temporel entre deux points homologues desdites courbes (ici deux sommets successifs) et T la période commune des deux signaux sinusoïdaux, on peut dire ceci :
A la période T correspond l'angle  2 radians;
à l'unité de temps correspond l'angle  2/T ;
et à l'écart de temps t correspond l'angle  2t/T , et cet angle est le déphasage entre les deux courbes, soit l'argument de l'impédance en cause.
C'est la formule précédemment citée.

Je crois que j'ai compris (je vais aller revoir ça de près). Cette formule est générale, ou elle s'applique juste dans ce cas précis ?

Qu'appelez-vous "angle de phase" ? A quoi cela correspond?

L'impédance d'un dipôle peut être définie sous forme complexe Z par l'expressio  Z = |Z|e^j.
|Z| est le module de l'impédance et son angle de phase. Ce dernier est le déphasage provoqué par le dipôle entre la tension (sinusoïdale) à ses bornes et le courant qui le traverse.
Lorsque   = 0 , il n'y a pas de déphasage entre le courant et la tension; le dipôle est alors un élément purement résistif.

D'accord, je crois que cette fois, j'ai les idées à peu près claires sur ces notions clés de l'électricité. Merci infiniment pour ces nombreuses explications détaillées.